2021年8月1日日曜日
2020年1月26日日曜日
論文読み「Your Classifier Is Secretly An Energy Based Model And You Should Treat It Like One」
はじめに
「Your Classifier Is Secretly An Energy Based Model And You Should Treat It Like One」をまとめる。
概要
Energy Based Model
パラメータ$\theta$を持つ同時確率分布$p_{\theta}({\bf x},y)$をボルツマン分布を用いて表す。 \begin{equation} p_{\theta}({\bf x},y)=\frac{\exp{ \left( -E_{\theta} ({\bf x},y) \right) } }{Z(\theta)} \label{eq1} \end{equation} $E_{\theta}({\bf x},y)$はエネルギーであり、その定義については後述する。$Z(\theta)$は次式で定義される分配関数である。 \begin{equation} Z(\theta)=\int dx\int dy \exp{ \left( -E_{\theta} ({\bf x},y) \right) } \label{eq2} \end{equation} 式(\ref{eq1})のように確率分布をボルツマン分布を用いて表すモデルを、Energy Based Modelと呼ぶ。式(\ref{eq1})を$y$について周辺化して \begin{equation} p_{\theta}({\bf x}) = \int dy\;p_{\theta}({\bf x},y) \label{eq3} \end{equation} を得る。いま、$p_{\theta}({\bf x})$に対してもボルツマン分布を仮定する。 \begin{equation} p_{\theta}({\bf x})=\frac{\exp{\left(-E_{\theta}({\bf x})\right)}}{Z(\theta)} \label{eq5} \end{equation} これを変形すると \begin{eqnarray} \exp{\left(-E_{\theta}({\bf x})\right)} &=& Z(\theta)p_{\theta}({\bf x})\nonumber\\ &=& Z(\theta) \int dy\;p_{\theta}({\bf x},y)\nonumber\\ &=& Z(\theta) \int dy \frac{\exp{ \left( -E_{\theta} ({\bf x},y) \right) }}{Z(\theta)}\nonumber\\ &=& \int dy \exp{ \left( -E_{\theta} ({\bf x},y) \right) } \label{eq6} \end{eqnarray} 両辺の対数を取り \begin{equation} E_{\theta}({\bf x})=-\ln{\left( \int dy \exp{ \left( -E_{\theta} ({\bf x},y) \right) } \right) } \label{eq7} \end{equation} を得る。ここまでの手順をまとめると以下のようになる。
- エネルギー$E_{\theta}({\bf x},y)$を与える。
- 式(\ref{eq1})から$p_{\theta}({\bf x},y)$を計算する。
- 式(\ref{eq7})から$E_{\theta}({\bf x})$を計算する。
- 式(\ref{eq5})から$p_{\theta}({\bf x})$を計算する。
エネルギーの定義
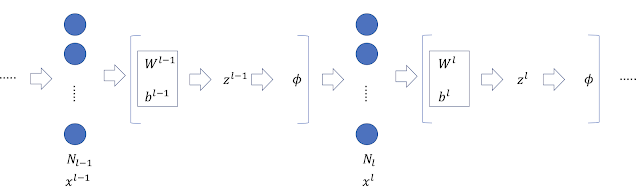
$E_{\theta}({\bf x},y)$について考えるため、従来の識別器の構成を示す（下の左図）。
最適化
学習時に最大化する目的関数は次式である。 \begin{equation} \ln{p_{\theta}({\bf x},y)}=\ln{p_{\theta}({\bf x})}+\ln{p_{\theta}(y|{\bf x})} \label{eq9} \end{equation} 第2項の最大化は従来とおりクロスエントロピーを用いれば良い。第1項の最大化については以下のようにする。最初に、式(\ref{eq5})の両辺の対数をとる。 \begin{equation} \ln{p_{\theta}({\bf x})}=-E_{\theta}({\bf x})-\ln{Z(\theta)} \end{equation} $\theta$で微分すると \begin{equation} \frac{\partial\ln{p_{\theta}({\bf x})}}{\partial\theta}=-\frac{\partial E_{\theta}({\bf x})}{\partial\theta} -\frac{1}{Z(\theta)}\frac{\partial Z(\theta)}{\partial\theta} \end{equation} ここで \begin{equation} Z(\theta)=\int dx \exp{\left(-E_{\theta}({\bf x})\right)} \end{equation} であるから、これを$\theta$で微分すると \begin{equation} \frac{\partial Z(\theta)}{\partial\theta}=\int dx \exp{\left(-E_{\theta}({\bf x})\right)}\left(-\frac{\partial E_{\theta}({\bf x})}{\partial\theta}\right) \end{equation} 故に \begin{eqnarray} \frac{1}{Z(\theta)}\frac{\partial Z(\theta)}{\partial\theta} &=& -\int dx \frac{\exp{\left(-E_{\theta}({\bf x})\right)}}{Z(\theta)} \left(\frac{\partial E_{\theta}({\bf x})}{\partial\theta}\right)\nonumber\\ &=& -\int dx p_{\theta}({\bf x}) \left(\frac{\partial E_{\theta}({\bf x})}{\partial\theta}\right)\nonumber\\ &=&-\mathbb{E}_{ p_{\theta}({\bf x}) } \left[ \frac{\partial E_{\theta}({\bf x})}{\partial\theta} \right] \end{eqnarray} となる。最後の等式は$p_{\theta}({\bf x})$による期待値であることを表す。以上から \begin{equation} \frac{\partial\ln{p_{\theta}({\bf x})}}{\partial\theta}=-\frac{\partial E_{\theta}({\bf x})}{\partial\theta} +\mathbb{E}_{ p_{\theta}({\bf x}) } \left[ \frac{\partial E_{\theta}({\bf x})}{\partial\theta} \right] \end{equation} を得る。$E_{\theta}({\bf x})$は式(\ref{eq7})により計算することができる。上式の第2項は分布$p_{\theta}({\bf x})$からサンプリングする必要がある。 本文献で使用するサンプリング手法は以下の通りである。 \begin{eqnarray} {\bf x}_{0}&\sim&p_0({\bf x}) \nonumber\\ {\bf x}_{i+1}&=&{\bf x}_i-\frac{\alpha}{2}\frac{\partial E_{\theta}({\bf x}_i)}{\partial {\bf x}_i}+\epsilon\nonumber\\ \epsilon&\sim&\mathcal{N}(0,\alpha) \end{eqnarray} ここで、$p_0({\bf x})$は一様分布である。本手法は、Stochastic Gradient Langevin Dynamics（SGLD）をベースにしたものである（詳細は略）。式(\ref{eq9})の第1項は教師なし学習、第2項は教師あり学習を行う。
実験
Hybrid Modelint
従来手法と比較したのが下図である。使用したデータセットは、CIFAR10である。
Calibration
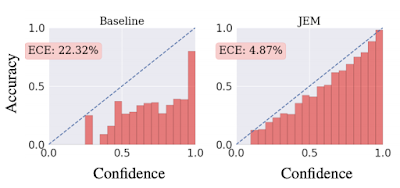
較正済み識別器（calibrated classifier）とは、$\max_y{p(y|{\bf x})}$（確信度）が正解率（accuracy）と比例するような識別器のことである。高い確信度を持って予測されたラベルは高い確率で正解となり、低い確信度で予測されたラベルは、誤認識である確率が高くなる。較正されているか否かを可視化する手順は以下の通り。
- データセット内の各サンプル${\bf x}_i$ごとに$\max_y{p(y|{\bf x}_i)}$を算出し、これらを等区間のバケットに振り分ける（ヒストグラムを作る）。例えば0から1までの区間を20等分した場合、20個のバケットに振り分ける。
- 各バケットに属するサンプルから平均精度を算出し、このバケットの高さとする。
較正度合いを定量化する指標が、次式で定義されるExpected Calibration Error（ECE）である。 \begin{equation} {\rm ECE}=\sum_{m=1}^{M}\frac{|B_m|}{n}|{\rm acc}(B_m)-{\rm conf}(B_m)| \end{equation} ここで、$M$はバケットの数、$n$はデータセット内のサンプル総数、$B_m$は１つののバケット中に格納されるサンプルの集合、$|B_m|$はサンプル数、${\rm acc}(B_m)$は集合$B_m$を用いて計算された平均精度、${\rm conf}(B_m)$は集合$B_m$を用いて計算された平均確信度である。${\rm ECE}$が小さくなるほど較正度合いは良くなり、完全に較正されている場合は0になる。上図に見るように、従来手法による識別器より、JEMで訓練した識別器の方が${\rm ECE}$は小さい。
Out-Of-Distribution Detection
分布外検知とは例えば以下のような識別器を作ることである（引用元）。
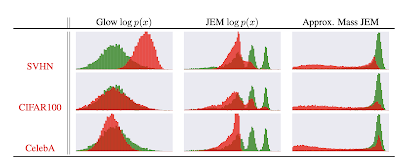
データセットCIFAR10で訓練した識別器に別の3つのデータセットSVHN、CIFAR100、CelebAを与えときのサンプルの対数分布（$\ln{p(x)}$）を示したのが下図である。
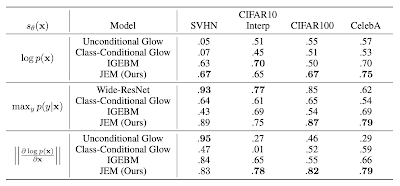
分布外検知に成功している多くの手法が採用している指標が次式である。 \begin{equation} s_{\theta}({\bf x})=\max_y{p_{\theta}(y|{\bf x})} \end{equation}
Robustness
JEMは敵対的サンプルに対しても頑健であると主張されている（詳細は略）。
まとめ
2019年2月24日日曜日
Reinforcement Learning An Introduction 第2版 4章
はじめに
テキストReinforcement Learning An Introduction 第2版の4章で紹介されている以下3つの手法をpythonで実装する。
- Iterative Policy Evaluation
- Policy Iteration
- Value Iteration
コードの場所
今回の全コードはここにある。
Iterative Policy Evaluation
この手法は状態価値関数$V(s)$についての次のベルマン方程式を使う。 \begin{equation} V(s)=\sum_{s^{\prime},a} P(s^{\prime}|s,a)\pi(a|s)\left[r(s,a,s^{\prime})+\gamma V(s^{\prime})\right] \label{eq1} \end{equation} この式の導出はここで行った。テキストに掲載されているIterative Policy Evaluationのアルゴリズムは以下の通りである（テキストPDF版から引用した）。
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from common import * # noqa
def update(v, state, gamma, reward):
updated_v = 0.0
for action in ACTIONS.values():
next_state = state + action
if not is_on_grid(next_state):
next_state = state
updated_v += 0.25 * (reward + gamma * v[next_state])
return updated_v
def main():
v = initialize_value_function(ROWS, COLS)
k = 0
while True:
delta = 0
for state in state_generator(ROWS, COLS):
if is_terminal_state(state):
continue
tmp = v[state]
v[state] = update(v, state, GAMMA, REWARD)
delta = max(delta, abs(tmp - v[state]))
k += 1
if delta < THRESHOLD:
break
print("iteration size: {}".format(k))
display_value_function(v)
if __name__ == "__main__":
main()
実行結果は以下である。
iteration size: 88 value funtion: [[ 0. -13.99330608 -19.99037659 -21.98940765] [-13.99330608 -17.99178568 -19.99108113 -19.99118312] [-19.99037659 -19.99108113 -17.99247411 -13.99438108] [-21.98940765 -19.99118312 -13.99438108 0. ]]小数点以下を四捨五入すれば、テキストの$k=\infty$の場合の数値と一致する。
Policy Iteration
この手法は、Policy Evaluationに対しては式(\ref{eq1})を、Policy Improvementに対しては次のベルマン最適方程式を使う。 \begin{equation} V^{*}(s)=\max_{a}\sum_{s^{\prime}} P(s^{\prime}|s,a)\left[r(s,a,s^{\prime})+\gamma V^{*}(s^{\prime})\right] \label{eq2} \end{equation} ただし、これをそのまま使うのではなく、次のようにしてpolicy更新のために利用する。 \begin{equation} \pi(a|s)={\rm arg}\max_{a}\sum_{s^{\prime}} P(s^{\prime}|s,a)\left[r(s,a,s^{\prime})+\gamma V(s^{\prime})\right] \label{eq3} \end{equation} 右辺を最大にするものが$N$個ある場合、各行動の実現確率を$1/N$とする。最大にしない行動には確率0を割り振る。 テキストにあるアルゴリズムは以下の通りである（PDF版から引用した）。
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as np
from common import * # noqa
def evaluate_policy(rows, cols, v, policy, gamma, reward, threshold):
while True:
delta = 0
for state in state_generator(rows, cols):
if is_terminal_state(state):
continue
tmp = v[state]
v[state] = update_value_function(v, policy, state, gamma, reward)
delta = max(delta, abs(tmp - v[state]))
if delta < threshold:
break
def update_value_function(v, policy, state, gamma, reward):
action_prob = policy[state]
updated_v = 0
for action_key, prob in zip(ACTIONS.keys(), action_prob):
next_state = state + ACTIONS[action_key]
if not is_on_grid(next_state):
next_state = state
updated_v += prob * (reward + gamma * v[next_state])
return updated_v
def update_policy(state, reward, gamma, v):
results = {}
for key in ACTIONS:
next_state = ACTIONS[key] + state
if not is_on_grid(next_state):
next_state = state
results[key] = reward + gamma * v[next_state]
max_vs = max(results.values())
return [k for k, val in results.items() if val == max_vs]
def improve_policy(rows, cols, policy, reward, gamma, v):
is_stable = True
for state in state_generator(rows, cols):
if is_terminal_state(state):
continue
old_action_prob = policy[state].copy()
new_policy = update_policy(state, reward, gamma, v)
overwrite_policy(state, new_policy, policy)
if not np.all(old_action_prob == policy[state]):
is_stable = False
return is_stable
def main():
v = initialize_value_function(ROWS, COLS)
policy = initialize_policy(ROWS, COLS)
while True:
evaluate_policy(ROWS, COLS, v, policy, GAMMA, REWARD, THRESHOLD)
is_stable = improve_policy(ROWS, COLS, policy, REWARD, GAMMA, v)
if is_stable:
break
display_policy(policy)
display_value_function(v)
if __name__ == "__main__":
main()
実行結果は以下の通り。
policy --- 0 1 left 0 2 left 0 3 down:left 1 0 up 1 1 up:left 1 2 up:right:down:left 1 3 down 2 0 up 2 1 up:right:down:left 2 2 right:down 2 3 down 3 0 up:right 3 1 right 3 2 right value function --- [[ 0. -1. -2. -3.] [-1. -2. -3. -2.] [-2. -3. -2. -1.] [-3. -2. -1. 0.]]policyの出力は、(行番号、列番号、矢印の向き)の順に並んでいる。
Value Iteration
本手法は式(\ref{eq2})を用いて状態価値関数$V(s)$を更新する。policy$（\pi(a|s)）$の決定には式(\ref{eq3})を使う。 テキストにあるアルゴリズムは以下の通りである（PDF版から引用した）。
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from common import * # noqa
import policy_iteration
def update(v, state, gamma, reward):
results = {}
for key in ACTIONS:
next_state = state + ACTIONS[key]
if not is_on_grid(next_state):
next_state = state
results[key] = reward + gamma * v[next_state]
max_vs = max(results.values())
return max_vs
def make_policy(v, rows, cols, reward, gamma):
policy = initialize_policy(rows, cols)
for state in state_generator(rows, cols):
if is_terminal_state(state):
continue
op = policy_iteration.update_policy(state, reward, gamma, v)
overwrite_policy(state, op, policy)
return policy
def main():
v = initialize_value_function(ROWS, COLS)
while True:
delta = 0
for state in state_generator(ROWS, COLS):
if is_terminal_state(state):
continue
tmp = v[state]
v[state] = update(v, state, GAMMA, REWARD)
delta = max(delta, abs(tmp - v[state]))
if delta < THRESHOLD:
break
policy = make_policy(v, ROWS, COLS, REWARD, GAMMA)
display_policy(policy)
display_value_function(v)
if __name__ == "__main__":
main()
実行結果の以下の通り。
policy --- 0 1 left 0 2 left 0 3 down:left 1 0 up 1 1 up:left 1 2 up:right:down:left 1 3 down 2 0 up 2 1 up:right:down:left 2 2 right:down 2 3 down 3 0 up:right 3 1 right 3 2 right value function --- [[ 0. -1. -2. -3.] [-1. -2. -3. -2.] [-2. -3. -2. -1.] [-3. -2. -1. 0.]]Policy Iterationのときと同じ結果である。
まとめ
「Policy Iteration」と「Value Iteration」の結果は同じになるが、テキストp.77に掲載されている矢印の向きと少し違う。異なる箇所は、2行3列目と3行2列目のマスである。 間違いが分かる方、ご指摘ください。
2018年11月30日金曜日
Conditional Random Field
はじめに
この文献をベースにしてCRFについてまとめる。
CRFモデル
いま、入力系列を$x_{1:N}(=x_1,\cdots,x_N)$、出力系列を$z_{1:N}(=z_1,\cdots,z_N)$と置き、下のグラフィカルモデルを考える。
素性関数（Feature Function）
指数関数の肩の部分を展開すると \begin{eqnarray} \sum_{n=1}^N\sum_{i=1}^F\lambda_i f_i\left(z_{n-1},z_n,x_{1:N},n\right) &=& \lambda_1\sum_{n=1}^N f_1\left(z_{n-1},z_n,x_{1:N},n\right)\\ &+& \lambda_2\sum_{n=1}^N f_2\left(z_{n-1},z_n,x_{1:N},n\right)\\ &+& \lambda_3\sum_{n=1}^N f_3\left(z_{n-1},z_n,x_{1:N},n\right)\\ &+& \cdots\nonumber\\ &+& \lambda_F\sum_{n=1}^N f_F\left(z_{n-1},z_n,x_{1:N},n\right)\nonumber\\ \end{eqnarray} となる。先に関数$f_i(\cdot)$はあらかじめ決めて置く量であると書いた。例えば以下のように与えることができる。 \begin{eqnarray} f_1\left(z_{n-1},z_n,x_{1:N},n\right)&=& \begin{cases} 1&\mbox{if $z_n$=PERSON and $x_n$=John}\\ 0&\mbox{otherwise} \end{cases}\\ f_2\left(z_{n-1},z_n,x_{1:N},n\right)&=& \begin{cases} 1&\mbox{if $z_n$=PERSON and $x_{n+1}$=said}\\ 0&\mbox{otherwise} \end{cases}\\ f_3\left(z_{n-1},z_n,x_{1:N},n\right)&=& \begin{cases} 1&\mbox{if $z_{n-1}$=OTHER and $z_{n}$=PERSON}\\ 0&\mbox{otherwise} \end{cases} \end{eqnarray} $f_1(\cdot)$は、同じ場所の入力値$x_n$と出力値$z_n$から決まる素性である。一方、$f_2(\cdot)$は、現在の出力値$z_n$と次の入力値$x_{n+1}$から決まる素性となっている。また、$f_3(\cdot)$は2つの隣接する出力値$z_{n-1},z_n$から決まる素性である。もちろん、$f_i(\cdot)$は2値である必要はなく、実数値を取る関数を与えることもできる。 いま \begin{eqnarray} F_1&=&\sum_{n=1}^N f_1\left(z_{n-1},z_n,x_{1:N},n\right) \\ F_2&=&\sum_{n=1}^N f_2\left(z_{n-1},z_n,x_{1:N},n\right) \\ F_3&=&\sum_{n=1}^N f_3\left(z_{n-1},z_n,x_{1:N},n\right) \end{eqnarray} などと置くと、指数型の部分は \begin{equation} \sum_{n=1}^N\sum_{i=1}^F\lambda_i f_i\left(z_{n-1},z_n,x_{1:N},n\right)=(\lambda_1,\cdots,\lambda_N) \cdot (F_1,\cdots,F_N)^T \end{equation} と書くことができる。$F=(F_1,\cdots,F_N)$を素性ベクトルと呼ぶ。
CRFの最適化
先に書いたようにCRFのパラメータ$\lambda_i$は学習により決まる量である。最尤推定法を用いる。 \begin{equation} L=\left(\prod_{j=1}^M p(z_{1:N}^{(j)}|x_{1:N}^{(j)})\right)p(\lambda_{1:F}) \end{equation} ただし、$\lambda_i$についての事前確率 \begin{eqnarray} p(\lambda_{1:F})&=&\prod_{i=1}^F p(\lambda_{i})\\ p(\lambda_{i})&=&\mathcal{N}(\lambda_i|0,\sigma^2) \end{eqnarray} を導入した。両辺対数を取れば \begin{equation} \ln{L}=\sum_{j=1}^M \ln{p(z_{1:N}^{(j)}|x_{1:N}^{(j)})}-\frac{1}{2}\sum_i^F\frac{\lambda_i^2}{\sigma^2} \end{equation} $\lambda_k$で微分する。 \begin{equation} \frac{\partial L}{\partial\lambda_k} = \sum_j\sum_n f_k(z_{n-1}^{(j)},z_n^{(j)},x_{1:N}^{(j)},n)- \frac{\partial}{\partial\lambda_k}\sum_j\ln{Z^{(j)}}- \frac{\lambda_k}{\sigma^2} \end{equation} ここで \begin{eqnarray} \frac{\partial\ln{Z^{(j)}}}{\partial\lambda_k} &=& \frac{1}{Z^{(j)}}\frac{\partial Z^{(j)}}{\partial\lambda_k}\\ &=& \sum_n\sum_{z_{n-1},z_n}p(z_{n-1},z_{n}|x_{1:N})f_k(z_{n-1}^{(j)},z_n^{(j)},x_{1:N}^{(j)},n)\\ &=& \sum_n\mathbb{E}_{z_{n-1},z_n} \left[ f_k(z_{n-1}^{(j)},z_n^{(j)},x_{1:N}^{(j)},n) \right] \end{eqnarray} 従って \begin{equation} \frac{\partial L}{\partial\lambda_k} = \sum_j\sum_n f_k(z_{n-1}^{(j)},z_n^{(j)},x_{1:N}^{(j)},n)- \sum_j\sum_n\mathbb{E}_{z_{n-1},z_n} \left[ f_k(z_{n-1}^{(j)},z_n^{(j)},x_{1:N}^{(j)},n) \right] - \frac{\lambda_k}{\sigma^2} \end{equation} を得る。解析的には解けないので、例えば、勾配降下法を用いて近似解を計算することになる。 \begin{equation} \lambda_k\leftarrow\lambda_k-\eta \frac{\partial L}{\partial\lambda_k} \end{equation}
2018年11月18日日曜日
ディープニューラルネットワークとガウス過程の関係
はじめに
ディープニューラルネットワークとガウス過程の関係をまとめる。先のページの続きである。
ディープニューラルネットワーク
以下のネットワークを考える。
ガウス過程との関係
$z^l_i$がガウス過程と等価となることを帰納法により証明する。
$l=0,1$のとき、先のページでの議論から$z^0_i$と$z^1_i$はガウス過程に従う量である。 いま、$z^{l-1}_i$がガウス過程に従う量であるとする。このとき、式(\ref{eq1})から$x_j^l$と$x_{j^{\prime}}^l$は、$j\neq j^{\prime}$のとき、独立である。式(\ref{eq2})から$z_i^l$は独立同分布から生成される項の和となるから、$N_l\rightarrow\infty$の極限で、$z_i^l$はガウス分布に従う（中心極限定理）。以上により、$z^l_i$がガウス過程と等価となることが証明された。ただし、$N_{0}\rightarrow\infty,N_{1}\rightarrow\infty,\cdots,N_{l-1}\rightarrow\infty,N_{l}\rightarrow\infty$の順に極限を取る必要がある。
平均と共分散行列の導出
$z^l_i$がガウス過程であることが示されたので、その平均と共分散行列を導く。平均は以下となる。 \begin{eqnarray} \mathbb{E}\left[z^l_i(x)\right] &=& \mathbb{E}\left[b_i^l\right]+\sum_{j=1}^{N_l}\mathbb{E}\left[W_{ij}^l x_j^l(x)\right]\\ &=& \mathbb{E}\left[b_i^l\right]+\sum_{j=1}^{N_l}\mathbb{E}_l\left[W_{ij}^l\right]\mathbb{E}_{l-1}\left[ x_j^l(x)\right] \end{eqnarray} ここで、$\mathbb{E}\left[b_i^l\right]=0,\mathbb{E}_l\left[W_{ij}^l\right]=0$であるから、$\mathbb{E}\left[z^l_i\right]=0$を得る。共分散行列は次式となる。 \begin{eqnarray} \mathbb{E}\left[z^l_i(x)z^l_i(x^{\prime})\right] &=& \mathbb{E}_l\left[b_i^l b_i^l\right]+ \sum_{j=1}^{N_l}\sum_{k=1}^{N_l} \mathbb{E}_l\left[W_{ij}^l W_{ik}^l\right] \mathbb{E}_{l-1}\left[x_j^l(x) x_k^l(x^{\prime})\right] \end{eqnarray} ここで \begin{eqnarray} \mathbb{E}_l\left[b_i^l b_i^l\right]&=&\sigma_b^2 \\ \mathbb{E}_l\left[W_{ij}^l W_{ik}^l\right]&=&\frac{\sigma_w^2}{N_l}\delta_{jk} \end{eqnarray} であるから \begin{eqnarray} \mathbb{E}\left[z^l_i(x)z^l_i(x^{\prime})\right] &=& \sigma_b^2+ \frac{\sigma_w^2}{N_l} \sum_{j=1}^{N_l} \mathbb{E}_{l-1}\left[x_j^l(x) x_j^l(x^{\prime})\right]\\ &=& \sigma_b^2+ \frac{\sigma_w^2}{N_l} \mathbb{E}_{l-1}\left[\sum_{j=1}^{N_l} x_j^l(x) x_j^l(x^{\prime})\right]\\ &=& \sigma_b^2+ \frac{\sigma_w^2}{N_l} \mathbb{E}_{l-1}\left[x^l(x)^T x^l(x^{\prime})\right]\\ &=& \sigma_b^2+ \frac{\sigma_w^2}{N_l} \mathbb{E}_{l-1}\left[ \phi\left(z^{l-1}\left(x\right)\right)^T \phi\left(z^{l-1}\left(x^{\prime}\right)\right) \right]\label{eq3}\\ &\equiv&K^l(x,x^{\prime}) \end{eqnarray} となる。$N$個の入力ベクトル$\left(x^{(1)},\cdots,x^{(N)}\right)$に対応する次の量 \begin{equation} {\bf z}_i^l=\left(z_i^l\left(x^{(1)}\right),\cdots,z_i^l\left(x^{(N)}\right)\right) \end{equation} は、ガウス分布$\mathcal{N}({\bf 0},K^l)$に従う。ここで、$K^l$の$(n,m)$成分は次式で与えられる。 \begin{equation} K_{nm}^l=K^l\left(x^{(n)},x^{(m)}\right) \end{equation} 式(\ref{eq3})の第2項にある期待値の計算を進める。表記を簡単にするため、$x^{(n)}$を$x_n$などと置くことにする。 \begin{eqnarray} A&\equiv& \mathbb{E}_{l-1}\left[ \phi\left(z^{l-1}\left(x_n\right)\right)^T \phi\left(z^{l-1}\left(x_m\right)\right) \right]\\ &=& \sum_{j=1}^{N_l}\mathbb{E}_{l-1}\left[ \phi\left(z^{l-1}_j\left(x_n\right)\right) \phi\left(z^{l-1}_j\left(x_m\right)\right) \right]\\ &=& \sum_{j=1}^{N_l} \int dz_j^{l-1}(x_1)\cdots dz_j^{l-1}(x_N) \phi\left(z^{l-1}_j\left(x_n\right)\right) \phi\left(z^{l-1}_j\left(x_m\right)\right)\\ &\times& \mathcal{N}(z_j^{l-1}(x_1)\cdots z_j^{l-1}(x_N)|{\bf 0},K^{l-1}) \end{eqnarray} 上の積分は、$z_j^{l-1}(x_n)$と$z_j^{l-1}(x_m)$以外の変数については実行できる。 \begin{eqnarray} A &=& \sum_{j=1}^{N_l} \int dz_j^{l-1}(x_n) dz_j^{l-1}(x_m) \phi\left(z^{l-1}_j\left(x_n\right)\right) \phi\left(z^{l-1}_j\left(x_m\right)\right)\\ &\times& \mathcal{N}(z_j^{l-1}(x_n),z_j^{l-1}(x_m)|{\bf 0},\Psi^{l-1}) \end{eqnarray} ここで \begin{equation} \Psi^{l-1}=\left( \begin{array}{cc} K^{l-1}_{nn} & K^{l-1}_{nm} \\ K^{l-1}_{mn} & K^{l-1}_{mm} \end{array} \right) \end{equation} とした。すなわち、$A$は3つの量、$K^{l-1}_{nn},K^{l-1}_{nm}(=K^{l-1}_{mn}),K^{l-1}_{mm}$と活性化関数$\phi$に依存する量であることがわかる。以上から \begin{equation} K^l_{nm}=\sigma_b^2+\sigma_w^2F_{\phi}(K^{l-1}_{nn},K^{l-1}_{nm},K^{l-1}_{mm}) \end{equation} と書くことができる。$F$は$\phi$の形が決まれば計算できる関数である。上の式から、$K^l$は$K^{l-1}$を用いて計算できることが分かる。
参考文献
Deep Neural Networks as Gaussian Processes
2018年11月10日土曜日
1層のニューラルネットワークとガウス過程の関係
はじめに
1層のニューラルネットワークとガウス過程の関係をまとめる。
1層のニューラルネットワーク
下図のニューラルネットワークを考える。
ガウス過程との関係
パラメータ$W^0_{jk}$と$b^0_j$はそれぞれ独立同分布から生成されると仮定したので、$x_j^1$と$x_{j^{\prime}}^1$は、$j\neq j^{\prime}$のとき、独立である。さらに、$z^1_i(x)$は独立同分布から生成される項の和であるから、$N_1\rightarrow\infty$の極限でガウス分布に従う（中心極限定理）。その分布の平均値は以下のように計算される。 \begin{eqnarray} \mathbb{E}\left[z^1_i(x)\right]&=& \mathbb{E}\left[b_i^1+\sum_{j=1}^{N_{1}}W^1_{ij}x_j^1(x)\right]\\ &=& \mathbb{E}\left[b_i^1\right]+\mathbb{E}\left[\sum_{j=1}^{N_{1}}W^1_{ij}x_j^1(x)\right]\\ &=& \mathbb{E}_1\left[b_i^1\right]+\sum_{j=1}^{N_{1}}\mathbb{E}_1\left[W^1_{ij}\right]\mathbb{E}_0\left[x_j^1(x)\right] \end{eqnarray} ここで$\mathbb{E}_l[\cdot]$は$W^l,b^l$の量で期待値を取ることを意味する。式(\ref{eq1}),(\ref{eq2})から次式が成り立つ。 \begin{eqnarray} \mathbb{E}_1\left[b_i^1\right]&=&0\\ \mathbb{E}_1\left[W^1_{ij}\right]&=&0 \end{eqnarray} したがって \begin{equation} \mathbb{E}\left[z^1_i(x)\right]=0 \end{equation} である。分散は次式のようになる。 \begin{eqnarray} \mathbb{E}\left[z^1_i(x)z^1_i(x^{\prime})\right]&=&\mathbb{E}\left[\left(b_i^1+\sum_{j=1}^{N_{1}}W^1_{ij}x_j^1(x)\right)\left(b_i^1+\sum_{k=1}^{N_{1}}W^1_{ik}x_k^1(x^{\prime})\right)\right]\\ &=&\mathbb{E}_1\left[b^1_i b^1_i\right]+\sum_j^{N_1}\sum_k^{N_1}\mathbb{E}_1\left[W^1_{ij}W^1_{ik}\right]\mathbb{E}_0\left[x^1_j(x)x^1_k(x^{\prime})\right] \end{eqnarray} 式(\ref{eq1}),(\ref{eq2})から次式が成り立つ。 \begin{eqnarray} \mathbb{E}_1\left[b^1_i b^1_i\right]&=&\sigma_b^2\\ \mathbb{E}_1\left[W^1_{ij}W^1_{ik}\right]&=&\frac{\sigma^2_w}{N_1}\delta_{jk} \end{eqnarray} 故に \begin{eqnarray} \mathbb{E}\left[z^1_i(x)z^1_i(x^{\prime})\right] &=&\sigma^2_b+\sum_j^{N_1}\sum_k^{N_1}\delta_{jk}\frac{\sigma^2_w}{N_1}\mathbb{E}_0\left[x^1_j(x)x^1_k(x^{\prime})\right]\\ &=&\sigma^2_b+\frac{\sigma^2_w}{N_1}\sum_j^{N_1}\mathbb{E}_0\left[x^1_j(x)x^1_j(x^{\prime})\right]\\ &=&\sigma^2_b+\sigma^2_w\;C(x,x^{\prime}) \\ &\equiv&K^1(x,x^{\prime}) \end{eqnarray} を得る。ただし \begin{eqnarray} C(x,x^{\prime}) &=&\frac{1}{N_1}\sum_j^{N_1}\mathbb{E}_0\left[x^1_j(x)x^1_j(x^{\prime})\right]\\ &=&\frac{1}{N_1}\mathbb{E}_0\left[\sum_j^{N_1}x^1_j(x)x^1_j(x^{\prime})\right]\\ &=&\frac{1}{N_1}\mathbb{E}_0\left[x^1(x)^T\cdot x^1(x^{\prime})\right] \end{eqnarray} と置いた。いま入力ベクトル$x$が$N$個あるとする。これを${\bf x}=(x^{(1)},\cdots,x^{(N)})$と書くことにする。このとき$z_i^1(x)$も$N$個並べることができる。 \begin{equation} {\bf z}_i^1=(z_i^1(x^{(1)}),\cdots,z_i^1(x^{(N)})) \end{equation} この${\bf z}_i^1$が、$N_1\rightarrow\infty$のとき、ガウス分布$\mathcal{N}({\bf z}_i^1|{\bf 0},K^1)$に従う量と等価となる。そして、共分散行列$K^1$の成分$K^1_{nm}$が次式で与えられる。 \begin{equation} K^1_{nm}=K^1(x^{(n)},x^{(m)}) \end{equation} ${\bf 0}\in \mathbb{R}^N, K^1\in \mathbb{R}^{N\times N}$である。
同じようにして$z_i^0(x)$の平均値を求めると \begin{eqnarray} \mathbb{E}\left[z^0_i(x)\right]&=& \mathbb{E}\left[b_i^0+\sum_{k=1}^{d_{in}}W^0_{ik}x_k\right]\\ &=& \mathbb{E}\left[b_i^0\right]+\mathbb{E}\left[\sum_{k=1}^{d_{in}}W^0_{ik}x_k\right]\\ &=& \mathbb{E}_0\left[b_i^0\right]+\sum_{k=1}^{d_{in}}\mathbb{E}_0\left[W^0_{ij}\right]x_k\\ &=&0 \end{eqnarray} となり、分散は \begin{eqnarray} \mathbb{E}\left[z^0_i(x)z^0_i(x^{\prime})\right] &=&\mathbb{E}\left[\left(b_i^0+\sum_{k=1}^{d_{in}}W^0_{ik}x_k\right)\left(b_i^0+\sum_{j=1}^{d_{in}}W^0_{ij}x_j^{\prime}\right)\right]\\ &=&\mathbb{E}\left[b_i^0 b_i^0\right]+ \sum_{k=1}^{d_{in}}\sum_{j=1}^{d_{in}}\mathbb{E}_0\left[ W^0_{ik}W^0_{ij} \right]x_k x_j^{\prime}\\ &=& \sigma_b^2+ \sum_{k=1}^{d_{in}}\sum_{j=1}^{d_{in}} \frac{\sigma_w^2}{d_{in}}\delta_{kj} x_k x_j^{\prime}\\ &=& \sigma_b^2+ \frac{\sigma_w^2}{d_{in}}\sum_{k=1}^{d_{in}} x_k x_k^{\prime}\\ &=& \sigma_b^2+ \frac{\sigma_w^2}{d_{in}} x^T\cdot x^{\prime}\\ &\equiv&K^0(x,x^{\prime}) \end{eqnarray} となる。 すなわち、${\bf z}_i^0$は、ガウス分布$\mathcal{N}({\bf z}_i^0|{\bf 0},K^0)$に従う量となる
参考文献
Deep Neural Networks as Gaussian Processes
2018年11月6日火曜日
ベイズ推論とガウス過程
はじめに
ベイズ推論とガウス過程の関係を、回帰を例に取り確認する。
ベイズ線形回帰
まず最初にベイズ推論を用いて線形回帰を考察する。いま観測値$X$と$Y$が与えられているとする。 \begin{eqnarray} X&=&\{x_1,\cdots,x_N\},x_n\in \mathbb{R}^M \\ Y&=&\{y_1,\cdots,y_N\},\;y_n\in\mathbb{R} \end{eqnarray} このとき次の尤度を考える。 \begin{equation} p(y_n|x_n,w)=\mathcal{N}(y_n|w^T\phi(x_n),\beta^{-1}) \end{equation} ここで、$\mathcal{N}(y_n|\mu,\sigma^2)$は平均$\mu$、分散$\sigma^2$の正規分布を表す。$w$はパラメータ($w\in\mathbb{R}^D$)、$\phi(\cdot)$は$M$次元空間内の点を$D$次元空間内の点に射影する関数である。次に、$w$の事前分布を次のように導入する。 \begin{equation} p(w)=\mathcal{N}(w|0,\alpha^{-1}I_D) \end{equation} $I_D$は$D\times D$の単位行列である。このとき事後分布$p(w|X,Y)$は厳密に計算でき \begin{eqnarray} p(w|X,Y)&=&\mathcal{N}(w|m,S) \\ m&=&S\beta\Phi^Ty \in \mathbb{R}^D\\ S&=&(\alpha I_D+\beta\Phi^T\Phi)^{-1} \in \mathbb{R}^{D\times D} \end{eqnarray} を得る。$y=(y_1,\dots,y_N)^T$、$\Phi$は$\Phi_{nd}=\phi_d(x_n)$を成分に持つ$N\times D$行列である。さらに、この事後分布から予測分布を求めることができる。 \begin{eqnarray} p(y_{*}|x_{*},X,Y)&=&\mathcal{N}(y_{*}|m^T\phi(x_*),\sigma^2(x_*)) \label{eq1}\\ \sigma^2(x_*)&=&\beta^{-1}+\phi^T(x_*)S\phi(x_*) \end{eqnarray} 以上が、ベイズ推論による線形回帰の結果である。
ガウス過程による回帰
いま観測値$X$と$Y$が与えられているとする。 \begin{eqnarray} X&=&\{x_1,\cdots,x_N\},x_n\in \mathbb{R}^M \\ Y&=&\{y_1,\cdots,y_N\},\;y_n\in\mathbb{R} \end{eqnarray} 観測値$X$と$Y$の間には次の関係があるとする。 \begin{equation} y_n=z(x_n)+\epsilon_n \end{equation} $\epsilon_n$が正規分布に従うノイズであれば次の尤度を考えることができる。 \begin{equation} p(y_n|z_n)=\mathcal{N}(y_n|z_n,\beta^{-1}) \end{equation} ただし、$z_n=z(x_n)$とした。観測値は独立同分布から生成されると仮定すれば次式を得る。 \begin{eqnarray} p(y|z) &=&p(y_1,\dots,y_N|z_1,\cdots,z_N) \\ &=&\prod_{n=1}^N p(y_n|z_n) \\ &=&\prod_{n=1}^N \mathcal{N}(y_n|z_n,\beta^{-1}) \\ &=&\mathcal{N}(y|z,\beta^{-1}I_N) \end{eqnarray} ただし、$y=(y_1,\dots,y_N)^T$、$z=(z_1,\dots,z_N)^T$と置いた。$I_N$は$N\times N$の単位行列である。ここで、$z$がガウス過程から生成される量であると仮定すると、次の事前分布を使うことができる。 \begin{equation} p(z)=\mathcal{N}(z|0,K) \end{equation} 共分散行列$K$のサイズは$N\times N$であり、その成分は次式で定義される。 \begin{equation} K_{nm}=k(x_n,x_m) \end{equation} $k(x_n,x_m)$は2点から1つのスカラー量が決まる関数であり、カーネル関数と呼ばれる。これらを用いて、$p(y,z)$を$z$について周辺化する。 \begin{eqnarray} p(y)&=&\int dz\;p(y|z)\;p(z)\\ &=&\mathcal{N}(y|0,C) \end{eqnarray} $C$は$N\times N$の行列であり、その成分は次式で与えられる。 \begin{equation} C_{nm}=k(x_n,x_m)+\beta^{-1}\delta_{nm} \end{equation} 予測分布は次のようなる。 \begin{eqnarray} p(y_*|x_*,X,Y)&=&\mathcal{N}(y_*|m^{'}(x_*),\sigma^{'\;2}(x_*)) \label{eq2}\\ m^{'}(x_*)&=&k^TC^{-1}y \\ \sigma^{'\;2}(x_*)&=&c-k^TC^{-1}k \end{eqnarray} ただし \begin{eqnarray} k&=&(k(x_n,x_*),\cdots,k(x_N,x_*))^T \\ c&=&k(x_*,x_*)+\beta^{-1} \end{eqnarray} である。以上がガウス過程による回帰の結果である。
ベイズ推論とガウス過程の関係
いま、カーネル関数が次式で定義されるとする。 \begin{equation} k(x_n,x_m)=\alpha^{-1}\phi^T(x_n)\phi(x_m) \end{equation} このとき、式(\ref{eq1})と(\ref{eq2})は等しくなる。
ベイズ推論による解法では$D$次元空間を考えるが、ガウス過程による解法では$N$次元空間を考える。前者では$D\times D$行列の逆行列を、後者では$N\times N$行列の逆行列を計算する必要がある。それぞれの計算量は$\mathcal{O}(D^3)$と$\mathcal{O}(N^3)$である。$D\lt N$である場合、パラメータ空間で計算した方が計算量は少なくなる。ガウス過程を使う利点は、$K$として様々なカーネルを使うことができる点である。
ガウス過程のハイパーパラメータの決定
いま共分散行列$K$がハイパーパラメータ$\theta$でモデル化されているとする。 \begin{equation} p(z|\theta)=\mathcal{N}(z|0,K_{\theta}) \end{equation} このとき \begin{eqnarray} p(y|\theta)&=&\int dz\;p(y|z)\;p(z|\theta)\\ &=&\mathcal{N}(y|0,C_{\theta}) \\ C_{\theta,nm}&=&K_{\theta,nm}+\beta^{-1}\delta_{nm} \end{eqnarray} が成り立つ。事前分布$p(\theta)$を考えると次式が成り立つ。 \begin{equation} p(\theta|y)=\frac{p(y|\theta)p(\theta)}{p(y)} \end{equation} 一般的に右辺分母は解析的に計算できないので、何らかの近似が必要になる。書籍「Pythonによるベイズ統計モデリング PyMCでのデータ分析実践ガイド」の第8章にPyMC3を用いた解法が掲載されている。
登録:
投稿 (Atom)