はじめに
先のページでは多層パーセプトロンを解説した。今回は、これを拡張することによりConvolutional Neural Networkを導く。
多層パーセプトロン
隠れ層が一層の多層パーセプトロンは以下のような構造であった。
これに対応する式は以下のように与えられる。
\begin{eqnarray}
y_k
&=&
\pi\left(\;f_k\left( \vec{z}; W^{(2)},\vec{b}^{\;(2)}\right)\;\right) \label{eprob-2}\\
\pi(a_k)
&=&
\frac{\exp{(a_k)}}
{\sum_{j=1}^{K}\;\exp{(a_j)}} \label{softmax-1}\\
\vec{f}\left( \vec{z}; W^{(2)},\vec{b}^{\;(2)}\right)
&=&
W^{(2)\;T}\;\vec{z} + \vec{b}^{\;(2)}\label{projection-2}
\end{eqnarray}
\begin{eqnarray}
z_h
&=&
\tanh\left(\;g_h\left( \vec{x}; W^{(1)},\vec{b}^{\;(1)}\right)\;\right) \label{eprob-1}\\
\vec{g}\left( \vec{x}; W^{(1)},\vec{b}^{\;(1)}\right)
&=&
W^{(1)\;T}\;\vec{x} + \vec{b}^{\;(1)}\label{projection-1}
\end{eqnarray}
ここで、
W^{(1)} は
D\times H 行列、
\vec{b}^{\;(1)} は
H 次元ベクトル、
W^{(2)} は
H\times K 行列、
\vec{b}^{\;(2)} は
K 次元ベクトルである。ただし、隠れ層の活性化関数として
\tanh{} を採用している。
最下層は入力層であり
D 個のユニットから構成される。隠れ層のユニット数は
H 個、最上層は出力層であり
K 個のユニットから構成される。これを適用する具体例として、
D 次元のベクトルとして与えられる観測値を
K 個のクラスのいずれかに分類する多分類問題を挙げることができる。
上図における層間の接続に注目したものが下図である。各ユニットは、下層の全ユニットと接続している。
Convolutional Neural Network(CNN)
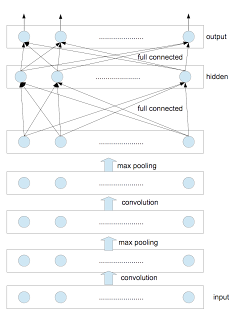
いま、入力層(input layer)と隠れ層(hidden layer)の間に複数の層を挿入する。
上図は、convolution layerと pooling layerの対を2つ挿入したものである。
一般に、この対を任意の数だけ挿入したものをconvolutional neural networkと呼ぶ。以下各層について説明する。
① convolution layer
多次元ロジスティック回帰や多層パーセプトロンでは、1次元のベクトルを入力値としてきたが、ここでは入力値として2次元ベクトルを考える。具体的には画像が入力値となる場合を考察する。まず最初に、
m 番目の入力画像の
l 番目のチャンネルを考え、位置
(i,j) にある画素
x_{m,l,i,j} について以下の計算を行なう。
\begin{equation}
g_{m,k,i,j} = \sum_{p,q,l} \; w_{k,l,p,q}\;x_{m,l,i+p,j+q}
\label{eq1}
\end{equation}
これは、矩形のフィルタ
w_{k,l} を使って convolution を行い、
l について和をとることと等価である。カラー画像なら
l の総数は3、グレースケールなら1である。convolution を
\circledast で表すことにすれば、式(
\ref{eq1})は
\begin{equation}
g_{m,k} = \sum_{l} \; w_{k,l} \circledast x_{m,l}
\label{eq2}
\end{equation}
と書くことができる。
② max pooling
次に行なう処理は pooling である。pooling の方法にはいくつかあるが、ここでは max pooling を取り上げる。max pooling とは、
画像を
a\times a の領域に細分し、各領域内の最大値でその領域を代表させる処理である。
a=2 なら
w\times hの画像は
w/2\times h/2 のサイズにダウンサンプリングされる。いま形式的に max pooling の処理を
p_{\rm{pooling}}(\cdot) と書くことにすれば、この処理の出力値は
\begin{equation}
q_{m,k} = p_{\rm{pooling}}\left(\sum_{l} \; w_{k,l} \circledast x_{m,l}\right)
\label{eq3}
\end{equation}
となる。
③ 活性化関数
ここまでの出力値
q_{m,k} にスカラー量であるバイアス項
b_{k} を加え、
\tanh で活性化する。
\begin{equation}
r_{m,k} = \tanh{(q_{m,k}+b_k)}
\label{eq4}
\end{equation}
出力値
r_{m,k} は、feature mapと呼ばれる。これを新たな入力値
x_{m,l} とみなして ①②③ の処理を繰り返す。その際、フィルタの数
k を変えることができる。たとえば、最初の処理①②③では20種類のフィルタを使い、次の処理①②③では50種類のフィルタを使うなどである。
convolution layerとpooling layerの対が2つ、最初の画像サイズが28
\times28、フィルタサイズが5
\times5の場合を考える。最初のconvolution layerにより画像サイズは 24
\times 24となり、それに引き続く pooling layer により画像サイズは12
\times12となる。次のconvolution layerへの入力画像のサイズは12
\times 12となり、フィルタサイズが最初と同じなら、convolution layerにより画像サイズは8
\times8、pooling layerにより画像サイズは4
\times4となる。2つ目のcovolution に使うフィルタの数が50なら、4
\times4の画像が50個出来上がる。すなわち、1枚の画像(サイズは28
\times28)から50組の16(=
4\times 4)画素が作成される。この画素を一列に並べた800(
=50\times 16)次元のベクトルを多層パーセプトロンのhidden layerの入力とみなす。あとの処理は
先のページと同じである。
計算を行なう際の留意点
- CNNの計算量はMLPと比べ著しく多くなる。
私のiMac(3.06GHz Intel Core 2 Duo, 4GB)で、参考文献にあるtheanoコードを実行したところ、MLPで8.32時間、CNNで20.99時間となった。0-1lossの値は、MLPで1.68%、CNNで0.91%であった。
- 各層の計算時間を同じにするため、(feature mapの数\timesfeature mapを構成する画素の数)を各層でほぼ同じにすることがよく行なわれる。
- 考察するデータセットごとに最適なフィルタサイズは変わる。入力画像が28\times28程度であれば5\times5のフィルタがよく使われる。一方、数百画素\times数百画素の画像に対しては12\times12や15\times15程度のフィルタを用いることが多い。
- max poolingを行なわない選択肢もある。行なうとしても、そのサイズは2\times2が限度である。これ以上のdownsamplingを行なうと、多くの情報が失われてしまう。
- whitening(白色化)を導入することにより識別率は高くなる。
- 確率的勾配降下法の各イテレーションごとに学習率を小さくすることにより収束速度を上げることができる。
まとめ
多次元ロジスティック回帰は入力層と出力層の2層からなるNeural Network、
多層パーセプトロンはこの2層の間に隠れ層を複数個挿入したNeural Network、そして、Convolutional Neural Networkは、多層パーセプトロンにconvolution層とpooling層の対を複数個挿入したNeural Networkである。多分類問題に適用した際の識別率は、一般的には、入力層と出力層の間の中間層が増える程高くなる。
参考文献
Convolutional Neural Networks (LeNet)
Theanoを使った実装が掲載されている。