Computational Geometry 〜 Symbolic Perturbation 〜

in Japanese

Introduction

　In the implementation of computational geometry algorithms, it is important to allow numerical calculation to precisely determine the geometric phase structure which depends on the sign of a function $f$. To make the precise judgement, we should use a multiple-precision integer rather than a floating point number in numerical calculation. If floating-point coordinates are given as an input to the algorithm, they just have to be multiplied by a large number and converted to approximated integers. Even if we employ the multiple-precision integer, however, it is impossible to determine the geometric phase structure when ${\rm sign}(f)=0$. The state is called a degeneracy, which occurs when some coordinate values are coincident with each other. It is the symbolic perturbation method that addresses it. In this page, we would like to describe a brief explanation on the method based on the book.

Degeneracy

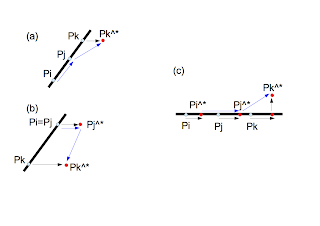
　In this explanation, we consider the following determinant: \begin{equation} F(P_i,P_j,P_k) = \left| \begin{array}{ccc} 1 & x_i & y_i \\ 1 & x_j & y_j \\ 1 & x_k & y_k \end{array} \right| \end{equation} where $P_i=(x_i,y_i)$, $P_j=(x_j,y_j)$, and $P_k=(x_k,y_k)$. In the case of a right-hand coordinate system, the determinant is used as follows:

When we follow a path $P_i \rightarrow P_j \rightarrow P_k$,

1. if $F(P_i,P_j,P_k) > 0$, the path turns left at $P_j$.
2. if $F(P_i,P_j,P_k) < 0$, the path turns right at $P_j$.

The judgement, for example, is used to implement the 2-dimensional convex hull algorithm as shown here. The degeneracy in the judgement occurs when $F(P_i,P_j,P_k) = 0$. In other words, there exists the point $P_k$ on the line through points $P_i$ and $P_j$ as shown below:

Symbolic Perturbation

　Suppose that the total number of points is $n$. We consider three points of them under the assumption that $i>j>k$. The perturbation is added to each point as follows: \begin{eqnarray} P_i^{\ast}&=&(x_i+\epsilon^{M^i},y_i+\epsilon^{M^{n+i}}) \nonumber \\ &\equiv&(x_i^{\ast},y_i^{\ast}) \end{eqnarray} where $M$ is a large integer and $\epsilon$ is a minutely small quantity. Because we assume $i>j>k$, the sequence of $\{y_i,y_j,y_k,x_i,x_j,x_k\}$ has an ascending order of perturbation amounts. The symbolic perturbation resolves the degeneracies by taking the following steps:

1. The coordinate value with the largest deviation, that is $x_k$ in the current example, is shifted. Then we trace the path $P_i \rightarrow P_j \rightarrow P_k^{\ast}$.
2. If we still have the degeneracy, the coordinate value with the second largest deviation, that is $x_j$ in the current example, is shifted. Then we trace the path $P_i \rightarrow P_j^{\ast} \rightarrow P_k^{\ast}$.
3. The same process is repeated until the degeneracy disappears.

Three degeneracies (a), (b), and (c) in the above figure are resolved as shown below,

where points after perturbations are colored in red, and the path $P_i \rightarrow P_j \rightarrow P_k$ after resolving the degeneracy in blue. The detail procedures to (a), (b), and (c) are as follows:

1. Only shifting $x_k$, the degeneracy is resolved.
2. The degeneracy is not resolved by merely shifting $x_k$. The coordinate with the second largest deviation, $x_j$, also must be shifted to resolve the degeneracy.
3. Since the values, $x_i$, $x_j$, and $x_k$ exist along the $x$ axis, the shifting them does not result in the resolution of the degeneracies. The resolution is achieved only when the coordinate with the next largest deviation, $y_k$, is shifted.

The expansion of $F(P^{\ast}_i,P^{\ast}_j,P^{\ast}_k)$ in power series of $\epsilon$ is as follows: \begin{eqnarray} F(P_i^{\ast},P_j^{\ast},P_k^{\ast}) &=& \left| \begin{array}{ccc} 1 & x_i & y_i \\ 1 & x_j & y_j \\ 1 & x_k & y_k \end{array} \right| \nonumber\\ &&- \left| \begin{array}{ccc} 1 & y_i \\ 1 & y_j \end{array} \right|\;\epsilon^{M^{k}} + \left| \begin{array}{ccc} 1 & y_i \\ 1 & y_k \end{array} \right|\;\epsilon^{M^{j}} - \left| \begin{array}{ccc} 1 & y_j \\ 1 & y_k \end{array} \right|\;\epsilon^{M^{i}}\nonumber\\ &&+ \left| \begin{array}{ccc} 1 & x_i \\ 1 & x_j \end{array} \right|\;\epsilon^{M^{n+k}} - \left| \begin{array}{ccc} 1 & x_i \\ 1 & x_k \end{array} \right|\;\epsilon^{M^{n+j}} + \left| \begin{array}{ccc} 1 & x_j \\ 1 & x_k \end{array} \right|\;\epsilon^{M^{n+i}}\nonumber\\ &&+ \epsilon^{M^{n+k}}(\epsilon^{M^{j}}-\epsilon^{M^{i}}) - \epsilon^{M^{n+j}}(\epsilon^{M^{k}}-\epsilon^{M^{i}}) + \epsilon^{M^{n+i}}(\epsilon^{M^{k}}-\epsilon^{M^{j}}) \label{epsilon_f} \end{eqnarray} The terms in the above expression are arranged in descending order of contributions to $F(P^{\ast}_i,P^{\ast}_j,P^{\ast}_k)$. The processes of resolving degeneracies in (a), (b), and (c) are interpreted by means of the expression as below:

1. The 1st term in the right-hand side is 0. The 2nd term ($\epsilon^{M^{k}}$'s term) resolves the degeneracy. Since the term has the negative sign, $F(P_i^{\ast},P_j^{\ast},P_k^{\ast})<0$. Therefore, the path turns right at $P_j$.
2. The 1st and 2nd terms in the right-hand side are 0. The contribution of the 3rd term ($\epsilon^{M^{j}}$'s term) resolves the degeneracy. Since the sign of the term is negative, $F(P_i^{\ast},P_j^{\ast},P_k^{\ast})<0$. Therefore, the path turns right at $P_j$.
3. The 1st to 4th terms in the right-hand side are all 0. The 5th term ($\epsilon^{M^{n+k}}$'s term) resolves the degeneracy. Since the term has the positive sign, $F(P_i^{\ast},P_j^{\ast},P_k^{\ast})>0$. Therefore, the path turns left at $P_j$.

Moreover, consider the situation that three points overlap as below:

In this case, the 1st to 7th terms in the right-hand side of eq.(\ref{epsilon_f}) are all zero. The 8th term is the contribution of the perturbation to $y_k$. Since $\epsilon^{M^{j}}-\epsilon^{M^{i}}>0$, the sign of the 8th term is positive. Therefore, $F(P_i^{\ast},P_j^{\ast},P_k^{\ast})>0$, so the path turns left at $P_j$.

　From the discussions stated above, the symbolic perturbation method turns out to be the powerful tool to resolve the degeneracies.

Reference

1. 計算幾何プログラミング, 杉原厚吉, 岩波書店 (written in Japanese)