Coatesの方法

in English

1. はじめに

　近年、Deep Learning の研究が盛んである。その中にはその高精度の原因を解明しようする研究もある。そのひとつが A.Coates らの "An Analysis of Single-Layer Networks in Unsupervised Feature Learning" である。今回これを実装し手元にある画像に適用してみたのでまとめます。

2. アルゴリズム

　このアルゴリズムを検証するには、3つの画像セットが必要である。

1. 特徴ベクトルを生成する関数を作るための画像セット（$S_{\rm unsupervised}$）
2. 訓練用画像セット（$S_{\rm training}$）
3. テスト用画像セット（$S_{\rm test}$）

今回は、1と2を同じ画像セットとした。以下、アルゴリズムの詳細を順に示す。

最初に、$S_{\rm unsupervised}$ を使用して以下を行う。

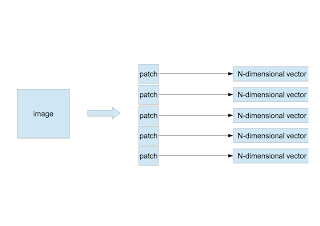
〜 パッチの切り出し 〜

1. 1枚の画像からサイズ $w \times w$ のパッチをランダムに $n$ 枚切り出す。
2. 1つのパッチの画素を左上から右下に向かって1列に並べ、$N$ 次元のベクトル $\vec{x}$ を作る。ここで $N=d\times w \times w$、$d$ は画像のチャンネル数である。カラー画像なら3、グレイ画像なら1である。
3. 複数枚の画像について同じことを繰り返す。画像が $m$ 枚あれば $N$ 次元ベクトルは $M(=n\times m)$ 個作られる( $\vec{x}^{\;\mu}, \mu=1,\cdots,M$ )。

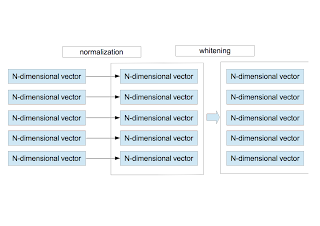
〜 正規化と白色化 〜

1. 現在、$M$ 個の$N$ 次元ベクトルがある。個々のベクトルに対し、その成分の平均値と分散を計算し、正規化を行う。 \begin{eqnarray} \bar{x}^{\mu}&=&\frac{1}{N}\sum_{i=1}^{N}x_{i}^{\mu} \nonumber \\ \sigma_{\mu}^2 &=& \frac{1}{N}\sum_{i=1}^{N}\left(x_{i}^{\mu} - \bar{x}^{\mu}\right)^{2} \nonumber \end{eqnarray} これらを使って、改めて $\vec{x}^{\;\mu}$ を定義し直す。 \begin{equation} x_{i}^{\mu} = \frac{x_{i}^{\mu} - \bar{x}^{\mu} }{ \sqrt{ \sigma_{\mu}^{2}+\epsilon_{\rm n} } } \end{equation} ここで、$\epsilon_{\rm n}$ は0割りを防ぐ微小量である。この作業は、局所領域（パッチ）内での明るさとコントラストの正規化に相当する。
2. 正規化された $M$ 個のベクトルを使って、白色化を行う。白色化の手順はここにまとめてある。

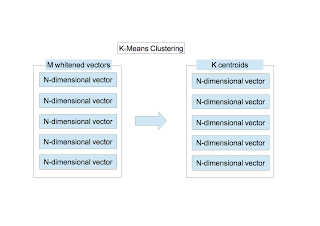
〜 クラスタリング 〜

　$M$ 個の $N$ 次元ベクトルに対し、$K$-meansクラスタリングを行う。クラスタリングの手順はここにまとめてある。$K$ 個の重心が求まる。

　下の画像は $K=1000$ としたときの961個の重心ベクトル（$N=36$次元ベクトル）を画像化したものである（成分の最小値を0に最大値を255に置き換え6$\times$6の画像に変換した）。

〜 特徴ベクトルの作成 〜

　ここまでの手順で以下のものが取得できた。

1. 白色化行列 $M_{\rm W}$
2. $K$ 個の重心座標 $\vec{c}_{\;k}, k=1,\cdots,K$

これらを使って、画像から取り出した1つのパッチから1つの特徴ベクトルを生成する関数を組み立てる。その手順は以下の通りである。

1. パッチの画素を左上から右下に向かって1列に並べ、$N$ 次元のベクトル $\vec{x}$ を作成する。
2. $\vec{x}$ を正規化する。
3. 正規化した $\vec{x}$ に白色化行列 $M_{\rm W}$ をかけて白色化する。$\vec{x}_{\rm W} = M_{\rm W}\;\vec{x}$
4. 関数 $f_{k}(\vec{x}_{\rm W})$ を次式で定義する。 \begin{equation} f_{k}(\vec{x}_{\rm W})=\max{\left(0, \mu(z)-z_k\right)} \nonumber \end{equation} ここで、 \begin{eqnarray} z_k&=&\|\vec{x}_{\rm W}-\vec{c}_{\;k} \| \nonumber \\ \mu(z)&=&\frac{1}{K}\sum_{k=1}^{K}z_k \nonumber \end{eqnarray} である。つまり、ある点 $\vec{x}_{\rm W}$ に注目したとき、この点と $K$ 個の重心との平均距離を算出する。 そして、平均距離より近い重心のインデックスには有限値を、遠い重心のインデックスには0を割り振る。 上の重心画像を使ってもう少し言い換えると、個々のパッチに対する各重心画像の寄与の度合いを表していることになる。 関数 $f_{k}$ により $N$ 次元ベクトルは、$K$ 次元ベクトルに変換される。これが特徴ベクトルである。

次に、$S_{\rm training}$ に対し以下を行う。

〜 訓練画像からの特徴ベクトルの抽出〜

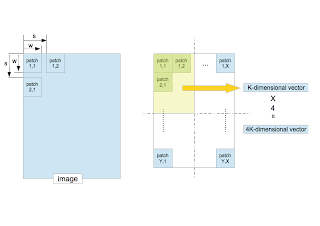
1. 1枚の訓練画像を考える。サイズ $w\times w$ のパッチを切り出す。その際、次のパッチとの距離（ストライド）を $s$ とする。左上から右下に向かって規則正しくパッチを取り出す。
2. 各パッチから $K$ 次元の特徴ベクトルを算出する。
3. 取り出したパッチが作る全領域を４等分し、各矩形に属する特徴ベクトルの平均ベクトルを計算する。この作業は、Deep LearningにおけるPoolingに相当する。識別対象の位置依存性を減らす手続きでもある。
4. 4つの $K$ 次元ベクトルを並べた4 $K$ 次元ベクトルを、画像1枚に対する特徴ベクトルとする。
5. 全ての訓練画像に対し同じことを繰り返す。訓練画像が $D$ 枚あれば、$D$ 個の4 $K$ 次元ベクトルが作られる。
6. これらを使って、SVMで訓練する。

　上の図を見れば明らかであるが、本手法はパッチの走査とPoolingがそれぞれ一度だけ行われる。また、パッチを特徴ベクトルへ変換する関数 $f_k$ は教師なし学習（$K$-meansクラスタリング）により得られる。よって、Single-Layer Networks in Unsupervised Feature Learning なのである。

最後に、$S_{\rm test}$ に対し以下を行う。

〜 テスト画像の評価 〜

1. 上と全く同じ手順で1枚の画像を4 $K$ 次元の特徴ベクトルに変換する。
2. SVMで識別する。

3. 実装

実装言語はC++、使用したライブラリは以下の通りである。

1. opencv2: 画像周りや $K$-meansクラスタリングなど。
2. boost::numeric::ublas: 白色化の計算など。
3. liblinear: 線形SVMを使った訓練とテスト。

また、アルゴリズムの各手順をつなぎ合わせる際、pythonを使用した。

4. 画像セット

　使用した画像セットはLSP15と呼ばれているものである。ここの scene category dataset という項目をクリックするとダウンロードできる。15個のカテゴリに分類された室内・室外画像である。各カテゴリには、縦横200から300ピクセル程度の画像が200から300枚ほど含まれている。
　今回の検証では、15個のカテゴリから適当に2つを選択し、画像セット $S_{\rm training}^{A/B}$、$S_{\rm test}^{A/B}$ を構成した。

category	training	test	label
A	1-150 ($S_{\rm training}^{A}$)	151-200 ($S_{\rm test}^{A}$)	-1
B	1-150 ($S_{\rm training}^{B}$)	151-200 ($S_{\rm test}^{B}$)	+1

ダウンロードした画像にはimage_0001.jpgのような番号を含む名前が付けられている。上の表の番号はこれを表す。 訓練画像は各カテゴリから150枚、テスト画像は50枚を選択した。 また、関数 $f_{k}$ を作るための画像セット $S_{\rm unsupervised}$は、$S_{\rm training}^{A} + S_{\rm training}^{B}$ とした。総数は300枚である。画像セットにはカラー画像も混ざっているが全てグレー画像に変換して検証を行った。

5. パラメータ

　各種パラメータの値は以下の通りである。

$n$	$w$	$s$	$K$	$\epsilon_{\rm n}$	$\epsilon_{\rm w}$
50	6	1	1000	10	0.1

ここで、$\epsilon_{\rm w}$ は白色化行列 $M_{\rm W}$ の0割りを防ぐ微小量である。 \begin{equation} M_{\rm W}=R\;\left(\Lambda+\epsilon_{\rm w}I\right)^{-1/2}\;R^{T} \label{eq7} \end{equation} ただし、$I$ は単位行列である。白色化行列の詳細はここにまとめてある。

6. 識別率

　結果を以下に示す。accuracyは通常の線形SVMを、accuracy(Hellinger Kernel)はHellinger Kernelを使用したときの識別率である。

category A	category B	accuracy	accuracy(Hellinger Kernel)
bedroom	CALsuburb	99%(99/100)	97%(97/100)
livingroom	industrial	94%(94/100)	97%(97/100)
MITforest	MITmountain	81%(81/100)	86%(86/100)
industrial	CALsuburb	88%(88/100)	97%(97/100)

　Hellinger Kernelは、特徴ベクトルの各成分の平方根を計算したあと線形SVMを適用すれば実現できる（Homogeneous Kernel Map）。

7. 考察

1. 線形SVMであるが全般的に識別率は高い。
2. 1つを除いて、Hellinger Kernelの効果は高い。
3. MITforestとMITmountainの組の識別率が他と比べて低いが、下のサンプル画像を見れば納得できると思う。
4. 特別な局所特徴アルゴリズムを使わなくても高い識別率を達成できている。局所特徴アルゴリズムの研究は廃れていくのだろうか？

以下に各カテゴリのテスト画像の例を示す。

〜 bedroom 〜

〜 livingroom 〜

〜 MITforest 〜

〜 industrial 〜

〜 MITmountain 〜

〜 CALsuburb 〜