in Japanese
Introduction
In this page, I describe a brief explanation on the algorithm of the 2-dimensional convex hull upon which I touched in
the previous page. I also show you my implementation of it in C++.
Algorithm
The algorithm discussed here is called
the Incremental Method which has the complexity of $O(n\log{n})$
1.
Input: A sequence of points, $A=\{P_1,P_2,\cdots,P_n\}$ (We call the suffixes the
original numbers)
Output: Convex Hull, $C(A)$
- Arrange points in ascending order of $x$-coordinate values.
We write the resultant sequence as $A^{\prime}=\{P_{(1)},P_{(2)},\cdots,P_{(n)}\}$ and call the suffixes the sorted numbers.
When two points have the same $x$-coordinate value, we arrange them in descending order of the original numbers.
We store the table $T_{{\rm sorted}\rightarrow{\rm original}}$ that maps the sorted number to the original one.
- Make a triangle consisting of the first three points of $A^{\prime}$ and write it as $C(\{P_{(1)},P_{(2)},P_{(3)}\})$.
Store two arrays $V_{\rm clockwise}$ and $V_{\rm counterclockwise}$ that allow us to follow points in clockwise order and counterclockwise order, respectively. For instance, if the sorted number $a$ is followed by $b$ when we trace the points in clockwise order, $V_{\rm clockwise}(a)=b$ holds.
- Add points sequentially from $(3)$ to $(n)$. Every time a point is inserted, the algorithm $X$ that is discussed later is executed.
- Finally we obtain the output $C(\{P_{(1)},P_{(2)},\cdots,P_{(n)}\})$.
The sequence of points obtained by $V_{\rm clockwise}$ or $V_{\rm counterclockwise}$ provides the convex hull to us.
The symbolic perturbation method discussed in
the previous page is used in the above algorithm. We add the perturbation to each point as follows:
\begin{eqnarray}
(x_i,y_i)&\rightarrow&(x_i+\epsilon^{M^i},y_i+\epsilon^{M^{n+i}}) \nonumber \\
&\equiv&(x_i^{\ast},y_i^{\ast})
\end{eqnarray}
where $n$ is the total number of points, $M$ is a large integer, and $\epsilon$ is a minutely small quantity.
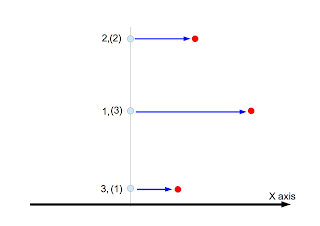
By selecting the
original number as the suffix $i$, even though $x$-coordinate values coincides with each other, we can sequentially add points in virtual ascending order of $x$-coordinate values. For example, we suppose that there are three points that have the same $x$-coordinate values shown in the below. In the figure, the number enclosed in parentheses indicates the
sorted number, and the number without them is the
original number.
Since the points with the same $x$-coordinate values are arranged in descending order of the
original numbers, the smaller the
sorted number is, the smaller the perturbation is.
The points after being perturbed are colored in red and the magnitude of the perturbation in blue in the figure.
Let us turn to the algorithm $X$.
Input:$C(\{P_{(1)},P_{(2)}, \cdots,P_{(k)}\})$, $P_{(k+1)}$, $V_{\rm clockwise}$, $V_{\rm counterclockwise}$, $T_{{\rm sorted}\rightarrow{\rm original}}$
Output:$C(\{P_{(1)},P_{(2)},\cdots,P_{(k+1)}\})$, $V_{\rm clockwise}$, $V_{\rm counterclockwise}$
- $P_{(s)}\leftarrow P_{(k)}$
- Consider three points, $P_{(k+1)}$, $P_{(s)}$, and $P_{(t)}$, where
$t=V_{\rm counterclockwise}(s)$.
- Trace these points in this order. If the path turns right at $P_{(s)}$, return to step 2 after setting $s\leftarrow t$. Otherwise return to step 4. See the figure below.
- Store the sorted number $(u)$ of the point at which the path turns left.
- $P_{(s)}\leftarrow P_{(k)}$
- Consider three points, $P_{(k+1)}$, $P_{(s)}$, and $P_{(t)}$, where $t=V_{\rm clockwise}(s)$.
- Trace these points in this order. If the path turns left at $P_{(s)}$, return to step 6 after setting $s\leftarrow t$. Otherwise return to step 8.
- Store the sorted number $(l)$ of the point at which the path turns right.
- Set $V_{\rm counterclockwise}(l)=k+1$ and $V_{\rm counterclockwise}(k+1)=u$.
- Set $V_{\rm clockwise}(u)=k+1$ and $V_{\rm clockwise}(k+1)=l$.
In order to determine if the path turns left or right, the determinant $F$ as shown in
the previous page is used.
- Consider $F(P_{(i)},P_{(j)},P_{(k)})$.
- Convert the sorted numbers to the original ones using $T_{{\rm sorted}\rightarrow{\rm original}}$.
\begin{eqnarray}
a&=&T_{{\rm sorted}\rightarrow{\rm original}}(i) \nonumber \\
b&=&T_{{\rm sorted}\rightarrow{\rm original}}(j) \nonumber \\
c&=&T_{{\rm sorted}\rightarrow{\rm original}}(k) \nonumber
\end{eqnarray}
- Arrange the elements of the list $L=(a,b,c)$ in descending order to generate a new list $L^{\prime}=(a^{\prime},b^{\prime},c^{\prime})$. If the conversion is done with an odd permutation, $p=-1$. Otherwise $p=1$.
- Calculate the value of $F(P_{a^{\prime}},P_{b^{\prime}},P_{c^{\prime}})$. Multiply its sign by $p$ to obtain the sign of $F(P_{a},P_{b},P_{c})$. If it is positive, the path turns left, otherwise turns right.
Implementation in C++
Here is my source code.The function
main is as follows:
- the 16th-39th lines: The input points are randomly generated.
- the 43th line: An object of the template class
ConvexHull2d is created. In this sample, the type of int is passed to the template argument. It is also possible to pass the type of boost::multiprecision::cpp_int to the template argument.
- the 44th line: The algorithm is executed.
- after the 46th line: The input points and the convex hull are drawn.
- the 57th line: The sequence of points which constitutes the convex hull is extracted.
Demos
Development Environment
- Mac OS X 10.8.4
- Processor:3.06 GHz Intel Core 2 Duo
- Memory:4GB
- Xcode4.6.2 with Apple LLVM 4.2(C++ Language Dialect → C++11, C++ Standard Library → libc++)
- boost-1.53.0 built by Apple LLVM 4.2 (See here)
- opencv-2.4.5 built by Apple LLVM 4.2 (See here)
Reference
- 計算幾何プログラミング, 杉原厚吉, 岩波書店 (in Japanese)