はじめに
論文
Adversarial Variational Bayesの前半部分の解説とChainerによる実装を行う。
論文概要
深層学習において生成モデルを求める代表的な手法は、Generative Adversarial Network(GAN)とVariational AutoEncoder(VAE)である。最初にGANが最適化する目的関数を示す。
\begin{equation}
\min_{\theta}\max_{\phi}
\left\{
{\rm E}_{p_{d}(x)}\left[\log{D_{\phi}(x)}\right]+{\rm E}_{p(z)}\left[1-\log{D_{\phi}\left(G_{\theta}(z)\right)}\right]
\right\}
\end{equation}
ここで、$p_d(x)$と$p(z)$はそれぞれ観測値$x$と潜在変数$z$の分布を表す。 ${\rm E}_{p}\left[\cdot\right]$は分布$p$による期待値である。$D_{\phi}$は識別器、$G_{\theta}$は生成器であり、それぞれパラメータ$\phi$と$\theta$で象徴される重みを持つネットワークである。上の式は次の2つの最適化を行うことを表す。
- $\theta$を固定して考える。観測値$x$と生成器$G_{\theta}(z)$の出力値を識別器$D_{\phi}$に与えたとき、$D_{\phi}(x)$の値を最大にし、$D_{\phi}(G_{\theta}(z))$の値を最小にするような$\phi$を見つける。
- $\phi$を固定して考える。観測値$x$と生成器$G_{\theta}(z)$の出力値を識別器$D_{\phi}$に与えたとき、$D_{\phi}(x)$の値を最小にし、$D_{\phi}(G_{\theta}(z))$の値を最大にするような$\theta$を見つける。
訓練の後、生成モデル$G_{\theta}(z)$を得ることになる。一方、VAEが最適化すべき式は次式である。
\begin{equation}
\max_{\theta}
\max_{\phi}
\left\{
-{\rm KL}
\left(
q_{\phi}(z|x),
p(z)
\right)
+
{\rm E}_{q_{\phi}(z|x)}
\left[\ln{p_{\theta}(x|z)}\right]
\right\}
\end{equation}
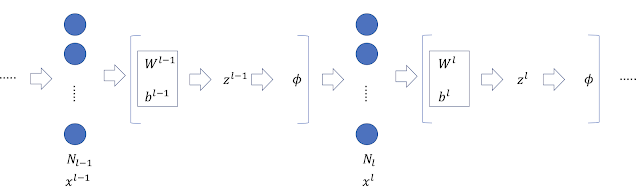
${\rm KL}$はKullback Leibler divergence、$q_{\phi}(z|x)$は観測値$x$が与えられた下での潜在変数$z$の事後確率を近似する分布である。上式第1項は正則化項、第2項は尤度を表す。すなわち、正則化項を考慮して尤度を最大化することになる。訓練の後、$q_{\phi}(z|x)$が推論モデル(inference model)、$p_{\theta}(x|z)$が生成モデル(generative model)になる。VAEの処理の流れを以下に示す。
GANとVAEを比べると、後者からは生成モデル以外に推論モデルも求めることができる。また、GANで決まる生成器は決定論的な関数であるが、VAEから求まる生成器は確率モデルである。さらに、GANには尤度に相当する量が存在せず、VAEには識別器に相当する仕組みが存在しない。
GANを自然画像に適用すると、シャープな画像を生み出すが、VAEではボケた画像になることが知られている。これは、VAEの推論モデル$q_{\phi}(z|x)$が真の事後確率$p(z|x)$を再現できていないためである。今回紹介する文献は、任意の形状を持つ推論モデルを扱うことのできる手法(Adversarial Variational Bayes:AVB)を提案している。本文献の主張をまとめると次のようになる。
- 任意の複雑な推論モデルを扱うことができる。
- VAEの目的関数に数学的な変換を施すことによりGAN的な目的関数を導出する。すなわち、VAEに識別器に相当する量が導入される。
- 上の目的関数は、ある極限の下で、VAEの元の目的関数と厳密に一致する。
論文詳細
観測値$x$の分布$p(x)$を考え、潜在変数$z$を導入する。
\begin{eqnarray}
\ln{p(x)}
&=&\ln\int dz\;p(x|z)p(z) \\
&=&\ln\int dz\;q(z|x) \frac{p(x|z)p(z)}{q(z|x)}
\end{eqnarray}
Jensenの不等式を用いて
\begin{eqnarray}
\ln{p(x)}
&\geqq&\int dz\;q(z|x) \ln\frac{p(x|z)p(z)}{q(z|x)} \\
&=&\int dz\;q(z|x)\ln{p(x|z)}-\int dz\;q(z|x)\ln{\frac{q(z|x)}{p(z)}} \\
&=&{\rm E}_{q(z|x)}\left[\ln{p(x|z)}\right]-{\rm KL}\left[q(z|x),p(z)\right] \\
&\equiv&\mathcal{L}
\end{eqnarray}
を得る。上式右辺はEvidence Lower Bound(ELOB)と呼ばれる量である。ここで、次の量を考える。
\begin{eqnarray}
{\rm KL}\left(q(z|x),p(z|x)\right)
&=&\int dz\;q(z|x)\ln{\frac{q(z|x)}{p(z|x)}} \\
&=&\int dz\;q(z|x)\ln{\frac{p(x)q(z|x)}{p(x,z)}} \\
&=&\int dz\;q(z|x)\ln{\frac{p(x)q(z|x)}{p(x|z)p(z)}} \\
&=&\int dz\;q(z|x)\ln{p(x)}-\int dz\;q(z|x)\ln{p(x|z)}+{\rm KL}(q(z|x),p(z)) \\
&=&\ln{p(x)}-\int dz\;q(z|x)\ln{p(x|z)}+{\rm KL}(q(z|x),p(z)) \\
\end{eqnarray}
上式は先に定義したELBO($\mathcal{L}$)を用いると
\begin{equation}
{\rm KL}\left(q(z|x),p(z|x)\right)=\ln p(x)-\mathcal{L}
\end{equation}
と書くことができる。すなわち次式が成り立つ。
\begin{equation}
\ln p(x)=\mathcal{L}+{\rm KL}\left(q(z|x),p(z|x)\right)
\end{equation}
$q(z|x)$は分布$p(z|x)$を近似するために導入された分布であり、パラメータ$\phi$を持つとする。一方、分布$p(x|z)$を表現するモデルはパラメータ$\theta$を持つとする。これらパラメータを顕に書くと
\begin{eqnarray}
\ln p(x)&=&\mathcal{L}+{\rm KL}\left(q_{\phi}(z|x),p(z|x)\right) \label{eq2}\\
\ln p(x)&\geqq&\mathcal{L} \label{eq1}\\
\mathcal{L}&=&{\rm E}_{q_{\phi}(z|x)}\left[\ln{p_{\theta}(x|z)}\right]-{\rm KL}\left[q_{\phi}(z|x),p(z)\right]
\end{eqnarray}
となる。VAEでは式(\ref{eq1})の右辺を$\phi$と$\theta$について最大化する。式(\ref{eq2})から、$\ln p(x)=\mathcal{L}$が成り立つのは$q_{\phi}(z|x)=p(z|x)$となる時であることが分かるが、一般にこの等式が成り立つことはない。通常のVAEでは実際に計算を進める際、$q_{\phi}(z|x)$を正規分布で近似する。本文献では$q_{\phi}(z|x)$に対してそのような近似を行わない。
$\mathcal{L}$は以下のように書き換えることができる。
\begin{eqnarray}
\mathcal{L}
&=&{\rm E}_{q_{\phi}(z|x)}\left[\ln{p_{\theta}(x|z)}\right]-{\rm KL}\left[q_{\phi}(z|x),p(z)\right] \\
&=&{\rm E}_{q_{\phi}(z|x)}\left[\ln{p_{\theta}(x|z)}\right]-\int dz\;q_{\phi}(z|x)\ln{\frac{q_{\phi}(z|x)}{p(z)}} \\
&=&{\rm E}_{q_{\phi}(z|x)}\left[\ln{p_{\theta}(x|z)}\right]-\int dz\;q_{\phi}(z|x)
\left[
\ln{q_{\phi}(z|x)}-\ln{p(z)}
\right] \\
&=&{\rm E}_{q_{\phi}(z|x)}
\left[
\ln{p_{\theta}(x|z)}-\ln{q_{\phi}(z|x)}+\ln{p(z)}
\right]\\
\end{eqnarray}
従って、VAEの目的関数は
\begin{equation}
\max_{\theta}\max_{\phi}
{\rm E}_{q_{\phi}(z|x)}
\left[
\ln{p_{\theta}(x|z)}-\ln{q_{\phi}(z|x)}+\ln{p(z)}
\right]
\label{eq4}
\end{equation}
となる。ここまでは通常のVAEである。本文献では、ここで、関数$T^*(x,z)$を次式で導入する。
\begin{equation}
T^*(x,z)=\arg\max_{T}
\left\{
{\rm E}_{q_{\phi}(z|x)}
\left[
\ln{\sigma\left(T(x, z)\right)}
\right]
+
{\rm E}_{p(z)}
\left[
\ln{\left(1-\sigma\left(T(x, z)\right)\right)}
\right]
\right\}
\label{eq3}
\end{equation}
この式は、$q_{\phi}(z|x)$からサンプリングされた$z$のとき$T(x,z)$を大きくし、$p(z)$からサンプリングされた$z$のとき$T(x,z)$を小さくすることを意味する。すなわち、$T(x,z)$は$q_{\phi}(x|z)$と$p(z)$を識別する識別器である。実際に$T^*(x,z)$を求めるため、式(\ref{eq3})の期待値を積分に書き換える。
\begin{equation}
\int dz
\left[
q_{\phi}(z|x)
\ln{\sigma\left(T(x, z)\right)}
+
p(z)
\ln{\left(1-\sigma\left(T(x, z)\right)\right)}
\right]
\end{equation}
上式の被積分関数の最大値を求めるため、$a=q_{\phi}(z|x)$、$b=p(z)$、$t=\sigma\left(T(x,z)\right)$として次式を考える。
\begin{equation}
y=a\ln{t}+b\ln{(1-t)}
\end{equation}
両辺$t$で微分して
\begin{equation}
\frac{dy}{dt}=\frac{a}{t}-\frac{b}{1-t}
\end{equation}
右辺を0とおいて
\begin{equation}
t=\frac{a}{a+b}
\end{equation}
を得る。各変数を元に戻して計算すると
\begin{equation}
T(x,z)=\ln{q_{\phi}(z|x)}-\ln{p(z)}\equiv T^{*}(x,z)
\end{equation}
を得る。$T^{*}$を用いると、式(\ref{eq4})は以下のように書くことができる。
\begin{equation}
\max_{\theta}\max_{\phi}
{\rm E}_{q_{\phi}(z|x)}
\left[
\ln{p_{\theta}(x|z)}-T^{*}(x,z)
\right]
\label{eq5}
\end{equation}
ただし
\begin{equation}
T^{*}(x,z)=\arg{\max_{T}}
\left\{
{\rm E}_{q_{\phi}(z|x)}
\left[
\ln{\sigma\left(T(x, z)\right)}
\right]
+
{\rm E}_{p(z)}
\left[
\ln{\left(1-\sigma\left(T(x, z)\right)\right)}
\right]
\right\}
\label{eq6}
\end{equation}
である。式(\ref{eq5})と(\ref{eq6})に再パレメータ化トリックを用いると
\begin{eqnarray}
T^{*}(x,z)&=&\arg{\max_{T}}
\left\{
{\rm E}_{p(\epsilon)}
\left[
\ln{\sigma\left(T(x, z_{\phi}(x,\epsilon)\right)}
\right]
+
{\rm E}_{p(z)}
\left[
\ln{\left(1-\sigma\left(T(x, z)\right)\right)}
\right]
\right\} \\
(\theta^*,\phi^*)&=&\arg\max_{\theta,\phi}
{\rm E}_{p(\epsilon)}
\left[
\ln{p_{\theta}\left(x|z_{\phi}\left(x,\epsilon\right)\right)}-T^{*}\left(x,z_{\phi}\left(x,\epsilon\right)\right)
\right]
\label{eq7}
\end{eqnarray}
を得る。$p(\epsilon)$は標準正規分布とすれば良い。観測値の分布$p_d(x)$による期待値も考慮して最終的に次の2つの目的関数を考えることになる。
\begin{eqnarray}
T^{*}(x,z)&=&\arg{\max_{T}}
\left\{
{\rm E}_{p_d(x)}
{\rm E}_{p(\epsilon)}
\left[
\ln{\sigma\left(T(x, z_{\phi}(x,\epsilon)\right)}
\right]
+
{\rm E}_{p_d(x)}
{\rm E}_{p(z)}
\left[
\ln{\left(1-\sigma\left(T(x, z)\right)\right)}
\right]
\right\} \label{eq9}\\
(\theta^*,\phi^*)&=&\arg\max_{\theta,\phi}
{\rm E}_{p_d(x)}{\rm E}_{p(\epsilon)}
\left[
\ln{p_{\theta}\left(x|z_{\phi}\left(x,\epsilon\right)\right)}-T^{*}\left(x,z_{\phi}\left(x,\epsilon\right)\right)
\right]
\label{eq8}
\end{eqnarray}
上の2式が本文献の最初の手法である。$T$を最適化したあと$(\theta,\phi)$を最適化する。アルゴリズムが文献に掲載されている。

ニューラルネットワークで表現される量は次の3つである。
- $z_{\phi}(x,\epsilon)$
- $p_{\theta}(x|z)$のパラメータ
- $T_{\psi}(x,z)$
文献の図5は、本アルゴリズムを評価するために用いられた実験データである。4次元データであり1つの成分だけが1、残りが0のデータである。
図6は$z_{\phi}(z|x)$から求まる潜在変数$z$の分布である。実験データは4種類のベクトルからなる。それぞれのデータごとに対応する$z$が色分けされている。同じデータに対する従来のVAEの結果も示されている。AVBの方が密に分布していることが分かる。 VAEの方はそれぞれの分布がガウス分布しているように見える。
下の表1は、各種評価値である。
表中のlog-likelihoodは$\ln{p_{\theta}(x|z)}$を、reconstruction errorは観測値$x$と再構築した$x$の間のクロスエントロピーを表す。いずれの値も従来法より精度が上がっていることが分かる。ここまでが本文献の前半の内容である。
Chainerによる実装
ここからは、Chainerを用いて実際に実装を行い、上の図5に示された実験データから図6(b)の結果を再現するまでの様子を記載する。ソースコードは
ここにある。既存の実装として参考にしたのは以下の3つである。
- https://gist.github.com/poolio/b71eb943d6537d01f46e7b20e9225149
- https://github.com/gdikov/adversarial-variational-bayes
- https://github.com/LMescheder/AdversarialVariationalBayes
1はtensorflow、2はkeras、3は本文献の著者によるtensorflowによる実装である。
Encoder
まず最初にEncoder($z_{\phi}(x,\epsilon)$)の実装を示す(encoder.py内のコードである)。
class Encoder_2(chainer.Chain):
def __init__(self, x_dim, eps_dim, h_dim=512):
super(Encoder_2, self).__init__()
with self.init_scope():
self.l1 = L.Linear(x_dim + eps_dim, h_dim, initialW=xavier.Xavier(x_dim + eps_dim, h_dim))
self.l2 = L.Linear(h_dim, h_dim, initialW=xavier.Xavier(h_dim, h_dim))
self.l3 = L.Linear(h_dim, h_dim, initialW=xavier.Xavier(h_dim, h_dim))
self.l4 = L.Linear(h_dim, eps_dim, initialW=xavier.Xavier(h_dim, eps_dim))
def update(self, updates):
update_links(self, updates)
def __call__(self, xs, es, activation=F.relu):
xs = 2 * xs - 1
h = F.concat((xs, es), axis=1)
h = self.l1(h)
h = activation(h)
h = self.l2(h)
h = activation(h)
h = self.l3(h)
h = activation(h)
h = self.l4(h)
return h
- 入力値は観測値xsと標準正規分布からのサンプル値esである。
- 15行目:xsは0と1である。これを-1と1に置き換える。
- 16行目:xsとesを連結する。
- あとは、全結合層と活性化関数の繰り返しである。
- 出力層には活性化関数を適用しない。
- 活性化関数としてreluを採用した。
Decoder
次はDecoderである(decoder.py内のコードである)。実験データは0と1から構成されるので$p_{\theta}(x|z)$としてBernoulli分布を用いる。
\begin{eqnarray}
p_{\theta}(x|z)
&=&{\rm Bern}(x|\mu(z))\\
&=&\mu(z)^x(1-\mu(z))^{1-x}
\end{eqnarray}
Decoderはパラメータ$\mu(z)$を計算する。
class Decoder_1(chainer.Chain):
def __init__(self, z_dim, x_dim=1, h_dim=512):
super(Decoder_1, self).__init__()
with self.init_scope():
self.l1 = L.Linear(z_dim, h_dim, initialW=xavier.Xavier(z_dim, h_dim))
self.l2 = L.Linear(h_dim, h_dim, initialW=xavier.Xavier(h_dim, h_dim))
self.l3 = L.Linear(h_dim, h_dim, initialW=xavier.Xavier(h_dim, h_dim))
self.l4 = L.Linear(h_dim, x_dim, initialW=xavier.Xavier(h_dim, x_dim))
def update(self, updates):
update_links(self, updates)
def __call__(self, zs, activation=F.tanh, is_sigmoid=False):
h = self.l1(zs)
h = activation(h)
h = self.l2(h)
h = activation(h)
h = self.l3(h)
h = activation(h)
h = self.l4(h)
if is_sigmoid:
h = F.sigmoid(h)
return h
- 入力値は潜在変数zsである。
- 最終層にだけ仕掛けがしてある。訓練時はis_sigmoid=False、テスト時にはis_sigmoid=Trueとする。
Discriminator
次はDiscriminator($T_{\psi}(x,z)$)である(discriminator.py)。
class Discriminator_1(chainer.Chain):
def __init__(self, x_dim, z_dim, h_dim=512):
super(Discriminator_1, self).__init__()
self.h_dim = h_dim
with self.init_scope():
self.xl1 = L.Linear(x_dim, h_dim, initialW=xavier.Xavier(x_dim, h_dim))
self.xl2 = L.Linear(h_dim, h_dim, initialW=xavier.Xavier(h_dim, h_dim))
self.xl3 = L.Linear(h_dim, h_dim, initialW=xavier.Xavier(h_dim, h_dim))
self.zl1 = L.Linear(z_dim, h_dim, initialW=xavier.Xavier(z_dim, h_dim))
self.zl2 = L.Linear(h_dim, h_dim, initialW=xavier.Xavier(h_dim, h_dim))
self.zl3 = L.Linear(h_dim, h_dim, initialW=xavier.Xavier(h_dim, h_dim))
def update(self, updates):
update_links(self, updates)
def __call__(self, xs, zs, activation=F.relu):
xs = 2 * xs - 1
hx = self.xl1(xs)
hx = activation(hx)
hx = self.xl2(hx)
hx = activation(hx)
hx = self.xl3(hx)
hx = activation(hx)
hz = self.zl1(zs)
hz = activation(hz)
hz = self.zl2(hz)
hz = activation(hz)
hz = self.zl3(hz)
hz = activation(hz)
h = F.sum(hx * hz, axis=1) / self.h_dim
return h
- 入力値は観測値xsと潜在変数zsである。
- 18行目:xsは0と1である。これを-1と1に置き換える。
- 19行目から24行目:xsについての計算である。
- 26行目から31行目:zsについての計算である。
- 32行目:それぞれの結果の内積を取る。
$(\theta,\phi)$についての目的関数(式(\ref{eq8}))
式(\ref{eq8})を実装したものが以下である(phi_loss_calculator.py)。
class PhiLossCalculator_2(chainer.Chain):
def __init__(self, encoder, decoder, discriminator):
super(PhiLossCalculator_2, self).__init__()
with self.init_scope():
self.encoder = encoder
self.decoder = decoder
self.discriminator = discriminator
def __call__(self, xs, zs, es):
batch_size = xs.shape[0]
encoded_zs = self.encoder(xs, es)
ys = self.decoder(encoded_zs)
d_loss = F.bernoulli_nll(xs, ys) / batch_size
t_loss = F.sum(self.discriminator(xs, encoded_zs)) / batch_size
return t_loss + d_loss, encoded_zs
- 式(\ref{eq8})では最大化しているが、実装では符号を反転させて最小化させる。
$\psi$についての目的関数(式(\ref{eq9}))
式(\ref{eq9})を実装したものが以下である(psi_loss_calculator.py)。
class PsiLossCalculator_3(chainer.Chain):
def __init__(self, encoder, discriminator):
super(PsiLossCalculator_3, self).__init__()
with self.init_scope():
self.encoder = encoder
self.discriminator = discriminator
def __call__(self, xs, zs, es):
# batch_size = xs.shape[0]
encoded_zs = self.encoder(xs, es)
posterior = self.discriminator(xs, encoded_zs)
prior = self.discriminator(xs, zs)
a = F.sigmoid_cross_entropy(posterior, np.ones_like(posterior).astype(np.int32))
b = F.sigmoid_cross_entropy(prior, np.zeros_like(prior).astype(np.int32))
c = F.sum(a + b)
return c
- こちらの目的関数も符号を反転させて最小化させる。
訓練コード
訓練コードの一部を掲載する。
for epoch in range(args.epochs):
with chainer.using_config('train', True):
# shuffle dataset
sampler.shuffle_xs()
epoch_phi_loss = 0
epoch_psi_loss = 0
for i in range(batches):
xs = sampler.sample_xs()
zs = sampler.sample_zs()
es = sampler.sample_es()
# compute psi-gradient(eq.3.3)
update_switch.update_models(enc_updates=False, dec_updates=False,
dis_updates=True)
psi_loss = psi_loss_calculator(xs, zs, es)
update(psi_loss, psi_loss_calculator, psi_optimizer)
epoch_psi_loss += psi_loss
# compute phi-gradient(eq.3.7)
update_switch.update_models(enc_updates=True, dec_updates=True,
dis_updates=False)
phi_loss, _ = phi_loss_calculator(xs, zs, es)
update(phi_loss, phi_loss_calculator, phi_optimizer)
epoch_phi_loss += phi_loss
# end for ...
# see loss per epoch
epoch_phi_loss /= batches
epoch_psi_loss /= batches
# end with ...
print('epoch:{}, phi_loss:{}, psi_loss:{}'.format(epoch, epoch_phi_loss.data,
epoch_psi_loss.data))
epoch_phi_losses.append(epoch_phi_loss.data)
epoch_psi_losses.append(epoch_psi_loss.data)
# end for ...
- 文献に掲載されているアルゴリズム図をほぼ踏襲している。
- 15行目から19行目:目的関数(\ref{eq9})を更新する。その際、EncoderとDecoderの重みを固定する(15行目)。
- 22行目から26行目:目的関数(\ref{eq8})を更新する。その際、Discriminatorの重みを固定する(22行目)。
予測のためのコード
訓練後に実行するコートはpredict.pyである。掲載は略。
実行
次を実行する。
$> ./train.py
$> ./predict.py
結果
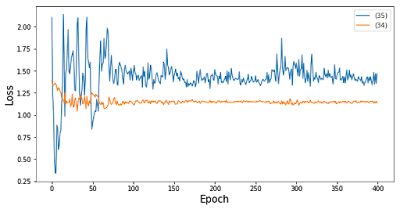
結果の表示はvisualize.ipynbで行った。最初に式(\ref{eq9})と(\ref{eq8})の変化を示す。
以下が学習後の$z_{\phi}(x,\epsilon)$の結果である。
Lossの振る舞いは良くわからないが、潜在変数$z$の分布は$(0,0)$を中心に綺麗に4分割されている。文献掲載の結果をそれなりに再現できているように見えるが。。。
まとめ
論文
Adversarial Variational Bayesの前半部分の解説と実装を示した。正直なところ、上のような形に到達するまでかなりの時間を費やして試行錯誤を繰り返した。2つの目的関数を交互に最適化するのは大変難しい。ご批判いただければ幸いである。