ディープニューラルネットワークとガウス過程の関係

はじめに

　ディープニューラルネットワークとガウス過程の関係をまとめる。先のページの続きである。

ディープニューラルネットワーク

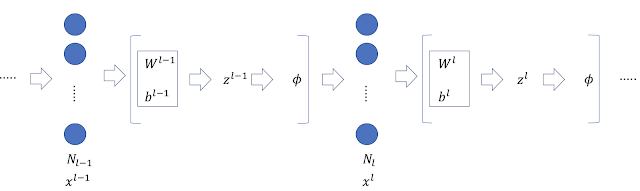
　以下のネットワークを考える。

各量の定義は以下の通り。 \begin{eqnarray} z^{l-1},x^{l}&\in& \mathbb{R}^{N_l} \\ z^{l}&\in&\mathbb{R}^{N_{l+1}}\\ \end{eqnarray} \begin{eqnarray} x_j^l(x)&=&\phi\left(z_j^{l-1}(x)\right)\label{eq1}\\ z_i^l(x)&=&b_i^l+\sum_{j=1}^{N_l}W_{ij}^l x_j^l(x)\label{eq2} \end{eqnarray}

ガウス過程との関係

　$z^l_i$がガウス過程と等価となることを帰納法により証明する。

　$l=0,1$のとき、先のページでの議論から$z^0_i$と$z^1_i$はガウス過程に従う量である。 いま、$z^{l-1}_i$がガウス過程に従う量であるとする。このとき、式(\ref{eq1})から$x_j^l$と$x_{j^{\prime}}^l$は、$j\neq j^{\prime}$のとき、独立である。式(\ref{eq2})から$z_i^l$は独立同分布から生成される項の和となるから、$N_l\rightarrow\infty$の極限で、$z_i^l$はガウス分布に従う（中心極限定理）。以上により、$z^l_i$がガウス過程と等価となることが証明された。ただし、$N_{0}\rightarrow\infty,N_{1}\rightarrow\infty,\cdots,N_{l-1}\rightarrow\infty,N_{l}\rightarrow\infty$の順に極限を取る必要がある。

平均と共分散行列の導出

　$z^l_i$がガウス過程であることが示されたので、その平均と共分散行列を導く。平均は以下となる。 \begin{eqnarray} \mathbb{E}\left[z^l_i(x)\right] &=& \mathbb{E}\left[b_i^l\right]+\sum_{j=1}^{N_l}\mathbb{E}\left[W_{ij}^l x_j^l(x)\right]\\ &=& \mathbb{E}\left[b_i^l\right]+\sum_{j=1}^{N_l}\mathbb{E}_l\left[W_{ij}^l\right]\mathbb{E}_{l-1}\left[ x_j^l(x)\right] \end{eqnarray} ここで、$\mathbb{E}\left[b_i^l\right]=0,\mathbb{E}_l\left[W_{ij}^l\right]=0$であるから、$\mathbb{E}\left[z^l_i\right]=0$を得る。共分散行列は次式となる。 \begin{eqnarray} \mathbb{E}\left[z^l_i(x)z^l_i(x^{\prime})\right] &=& \mathbb{E}_l\left[b_i^l b_i^l\right]+ \sum_{j=1}^{N_l}\sum_{k=1}^{N_l} \mathbb{E}_l\left[W_{ij}^l W_{ik}^l\right] \mathbb{E}_{l-1}\left[x_j^l(x) x_k^l(x^{\prime})\right] \end{eqnarray} ここで \begin{eqnarray} \mathbb{E}_l\left[b_i^l b_i^l\right]&=&\sigma_b^2 \\ \mathbb{E}_l\left[W_{ij}^l W_{ik}^l\right]&=&\frac{\sigma_w^2}{N_l}\delta_{jk} \end{eqnarray} であるから \begin{eqnarray} \mathbb{E}\left[z^l_i(x)z^l_i(x^{\prime})\right] &=& \sigma_b^2+ \frac{\sigma_w^2}{N_l} \sum_{j=1}^{N_l} \mathbb{E}_{l-1}\left[x_j^l(x) x_j^l(x^{\prime})\right]\\ &=& \sigma_b^2+ \frac{\sigma_w^2}{N_l} \mathbb{E}_{l-1}\left[\sum_{j=1}^{N_l} x_j^l(x) x_j^l(x^{\prime})\right]\\ &=& \sigma_b^2+ \frac{\sigma_w^2}{N_l} \mathbb{E}_{l-1}\left[x^l(x)^T x^l(x^{\prime})\right]\\ &=& \sigma_b^2+ \frac{\sigma_w^2}{N_l} \mathbb{E}_{l-1}\left[ \phi\left(z^{l-1}\left(x\right)\right)^T \phi\left(z^{l-1}\left(x^{\prime}\right)\right) \right]\label{eq3}\\ &\equiv&K^l(x,x^{\prime}) \end{eqnarray} となる。$N$個の入力ベクトル$\left(x^{(1)},\cdots,x^{(N)}\right)$に対応する次の量 \begin{equation} {\bf z}_i^l=\left(z_i^l\left(x^{(1)}\right),\cdots,z_i^l\left(x^{(N)}\right)\right) \end{equation} は、ガウス分布$\mathcal{N}({\bf 0},K^l)$に従う。ここで、$K^l$の$(n,m)$成分は次式で与えられる。 \begin{equation} K_{nm}^l=K^l\left(x^{(n)},x^{(m)}\right) \end{equation} 式(\ref{eq3})の第2項にある期待値の計算を進める。表記を簡単にするため、$x^{(n)}$を$x_n$などと置くことにする。 \begin{eqnarray} A&\equiv& \mathbb{E}_{l-1}\left[ \phi\left(z^{l-1}\left(x_n\right)\right)^T \phi\left(z^{l-1}\left(x_m\right)\right) \right]\\ &=& \sum_{j=1}^{N_l}\mathbb{E}_{l-1}\left[ \phi\left(z^{l-1}_j\left(x_n\right)\right) \phi\left(z^{l-1}_j\left(x_m\right)\right) \right]\\ &=& \sum_{j=1}^{N_l} \int dz_j^{l-1}(x_1)\cdots dz_j^{l-1}(x_N) \phi\left(z^{l-1}_j\left(x_n\right)\right) \phi\left(z^{l-1}_j\left(x_m\right)\right)\\ &\times& \mathcal{N}(z_j^{l-1}(x_1)\cdots z_j^{l-1}(x_N)|{\bf 0},K^{l-1}) \end{eqnarray} 上の積分は、$z_j^{l-1}(x_n)$と$z_j^{l-1}(x_m)$以外の変数については実行できる。 \begin{eqnarray} A &=& \sum_{j=1}^{N_l} \int dz_j^{l-1}(x_n) dz_j^{l-1}(x_m) \phi\left(z^{l-1}_j\left(x_n\right)\right) \phi\left(z^{l-1}_j\left(x_m\right)\right)\\ &\times& \mathcal{N}(z_j^{l-1}(x_n),z_j^{l-1}(x_m)|{\bf 0},\Psi^{l-1}) \end{eqnarray} ここで \begin{equation} \Psi^{l-1}=\left( \begin{array}{cc} K^{l-1}_{nn} & K^{l-1}_{nm} \\ K^{l-1}_{mn} & K^{l-1}_{mm} \end{array} \right) \end{equation} とした。すなわち、$A$は3つの量、$K^{l-1}_{nn},K^{l-1}_{nm}(=K^{l-1}_{mn}),K^{l-1}_{mm}$と活性化関数$\phi$に依存する量であることがわかる。以上から \begin{equation} K^l_{nm}=\sigma_b^2+\sigma_w^2F_{\phi}(K^{l-1}_{nn},K^{l-1}_{nm},K^{l-1}_{mm}) \end{equation} と書くことができる。$F$は$\phi$の形が決まれば計算できる関数である。上の式から、$K^l$は$K^{l-1}$を用いて計算できることが分かる。

参考文献

Deep Neural Networks as Gaussian Processes