はじめに
先のページでは1次元ロジスティック回帰について考察した。ここでは、多次元ロジスティック回帰を取り上げる。
多次元ロジスティック回帰
多分類問題を考える。$N$ 個の $D$ 次元ベクトル $\vec{x}^{\;n},n=1,\cdots,N$ が与えられ、それぞれが ${1,\cdots,K}$ のいずれかのラベルを持つとする。このとき、観測値が従う確率分布モデル $p(c=1,\cdots,K\;|\;\vec{x}\;;\;W,\vec{b})$ を求めたい。ここで、$W,\vec{b}$ はモデルを調節するパラメータである。$W$ は $D \times K$ 行列、$\vec{b}$ は $K$ 次元ベクトルである。各観測値が他の観測値の影響を受けないと仮定すれば、全ての観測値の確率は次式で与えられる。
\begin{equation}
L(W,\vec{b})=\prod_{n=1}^{N}\;p(c^{n}\;|\;\vec{x}^{\;n}\;;\;W,\vec{b})
\label{likelihood}
\end{equation}
これが最大となるように $(W,\vec{b})$ を調節すればよい。計算を容易にするため次式の最小化を考える。
\begin{equation}
L(W,\vec{b})=-\sum_{n=1}^{N}\;\ln{p(c^{n}\;|\;\vec{x}^{\;n}\;;\;W,\vec{b})}
\label{nll}
\end{equation}
上式を負の対数尤度(Negative Log Likelihood:NLL)関数と呼ぶ。確率 $p$ は次式で定義される。
\begin{equation}
p(c\;|\;\vec{x}\;;\;W,\vec{b})=\prod_{k=1}^{K}\;(y_k)^{t_k}
\label{prob}
\end{equation}
ここで、$y_k$ は $K$ 次元ベクトル $\vec{y}$ の $k$ 番目の成分、$t_k$ は $K$ 次元ベクトル $\vec{t}$ の $k$ 番目の成分である。$y_k$ は次式で定義される。
\begin{eqnarray}
y_k
&=&
\pi\left(\;f_k\left( \vec{x}; W,\vec{b}\right)\;\right) \label{eprob}\\
\pi(a_k)
&=&
\frac{\exp{(a_k)}}
{\sum_{j=1}^{K}\;\exp{(a_j)}} \label{softmax}\\
\vec{f}\left( \vec{x}; W,\vec{b}\right)
&=&
W^{T}\;\vec{x} + \vec{b}\label{projection}
\end{eqnarray}
行列やベクトルの肩にある $T$ は転置を表す。$\vec{f}$ は $K$ 次元ベクトルであり、$f_k$ はその $k$ 番目の成分を表す。
$\vec{t}$ は、観測値 $\vec{x}$ が持つラベルに相当する成分を1、それ以外の成分を0とする $K$ 次元ベクトルである。
たとえば、ラベル $3$ を持つなら
\begin{equation}
\vec{t} = (0,0,1,0,\cdots,0)^T
\end{equation}
となる。式(\ref{softmax})をsoftmax関数と呼ぶ。
$a_k={0,\cdots,9}$としたときのsoftmax関数を下に示す。
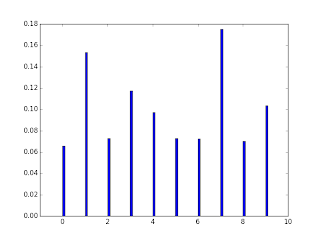
次式が成り立つことに注意する。
\begin{equation}
\sum_{k=1}^{K}\;\pi(a_k)=1
\end{equation}
すなわち、
\begin{equation}
\sum_{k=1}^{K}\;y_k=1
\end{equation}
ということであり、観測値 $\vec{x}$ はいずれかのラベルに必ず属するということである。
式(\ref{nll})に式(\ref{prob})を代入すると次式を得る。
\begin{equation}
L(W,\vec{b})=-\sum_{n=1}^{N}\;\sum_{k=1}^{K}
t_k^n\;\ln{(y_k^n)}
\end{equation}
ここまでの議論をまとめる。
- 式(\ref{projection})を使って、$D$次元ベクトル(観測値)を $K$ 次元ベクトルに射影する。
- $K$ 次元ベクトルの各成分を使って確率(\ref{softmax})を導入する。
- 確率的勾配降下法を用いて対数尤度を最小化し、最適なモデルを決定する。
計算を容易にするため、
$x^n_d,y^n_k,t^n_k$ を $x_{dn},y_{kn},t_{kn}$ に置き換え、これを行列の成分とみなすことにする。
\begin{equation}
L(W,\vec{b})=-\sum_{n=1}^{N}\;\sum_{k=1}^{K}
t_{kn}\;\ln{(y_{kn})}
\label{nllspecial}
\end{equation}
更新式
確率的勾配降下法については
先のページで説明したので、ここでは更新式だけを示す。
式(\ref{nllspecial})を $W$ の成分 $w_{dk}$ で微分する。
\begin{eqnarray}
\frac{\partial L}{\partial w_{dk}}
&=&
-\sum_{n=1}^{N}\;\sum_{s=1}^{K}\;t_{sn}\frac{1}{y_{sn}}\frac{\partial y_{sn}}{\partial a_{sn}}\frac{\partial a_{sn}}{\partial w_{dk}}
\end{eqnarray}
ここで、
\begin{eqnarray}
\frac{\partial y_{sn}}{\partial a_{sn}}&=&y_{sn}(1-y_{sn}) \\
\frac{\partial a_{sn}}{\partial w_{dk}}&=&x_{dn}\;\delta_{ks}
\end{eqnarray}
が成り立つので、これらを代入すると、
\begin{eqnarray}
\frac{\partial L}{\partial w_{dk}}
&=&
\sum_{n=1}^{N}\;t_{kn}(y_{kn}-1)\;x_{dn} \\
&=&
\sum_{n=1}^{N}\;(y_{kn}-t_{kn})\;x_{dn}
\end{eqnarray}
を得る。ただし、$t_{kn}\;y_{kn}=y_{kn}$ を用いた。同様に $b_k$ で微分すると次式を得る。
\begin{equation}
\frac{\partial L}{\partial b_{k}}
=
\sum_{n=1}^{N}\;(y_{kn}-t_{kn})
\end{equation}
いま、$e_{kn}=y_{kn}-t_{kn}$ と置くと
\begin{eqnarray}
\frac{\partial L}{\partial w_{dk}}
&=&
\sum_{n=1}^{N}\; x_{dn}\;e_{kn}\; \\
&=&
\left(X\;E^T\right)_{dk} \label{update1}\\
\frac{\partial L}{\partial b_{k}}
&=&
\sum_{n=1}^{N}\;e_{kn}
\label{update2}
\end{eqnarray}
となる。ここで $E$ は $e_{kn}$ を成分とする行列、$X$ は $x_{dn}$ を成分とする行列である。これらより更新式は以下のようになる。
\begin{eqnarray}
w_{dk} &\leftarrow& w_{dk} - \eta \; \left(X\;E^T\right)_{dk} \\
b_{k} &\leftarrow& b_{k} - \eta \; \sum_{n=1}^{N}\;e_{kn}
\end{eqnarray}
この更新式を使って、確率的勾配降下法を実行する。以下に各行列を書き下ろしておく。
\begin{eqnarray}
Y
&=&
\left(\begin{array}{cccc}
y_{11} & y_{12} & \cdots & y_{1N} \\
y_{21} & y_{22} & \cdots & y_{2N} \\
\vdots & \vdots & \ddots & \vdots \\
y_{K1} & y_{K2} & \cdots & y_{KN}
\end{array}
\right)
=
{\bf \pi}(W^T\;X+B)\label{pi}\\
\nonumber\\[3pt]
W
&=&
\left(\begin{array}{cccc}
w_{11} & w_{12} & \cdots & w_{1K} \\
w_{21} & w_{22} & \cdots & w_{2K} \\
\vdots & \vdots & \ddots & \vdots \\
w_{D1} & w_{D2} & \cdots & w_{DK}
\end{array}
\right)\\
\nonumber\\[3pt]
X
&=&
\left(\begin{array}{cccc}
x_{11} & x_{12} & \cdots & x_{1N} \\
x_{21} & x_{22} & \cdots & x_{2N} \\
\vdots & \vdots & \ddots & \vdots \\
x_{D1} & x_{D2} & \cdots & x_{DN}
\end{array}
\right)\\
\nonumber\\[3pt]
B
&=&
\left(\begin{array}{cccc}
b_{1} & b_{1} & \cdots & b_{1} \\
b_{2} & b_{2} & \cdots & b_{2} \\
\vdots & \vdots & \ddots & \vdots \\
b_{K} & b_{K} & \cdots & b_{K}
\end{array}
\right) \\
\nonumber\\[3pt]
T
&=&
\left(\begin{array}{cccc}
t_{11} & t_{12} & \cdots & t_{1N} \\
t_{21} & t_{22} & \cdots & t_{2N} \\
\vdots & \vdots & \ddots & \vdots \\
t_{K1} & t_{K2} & \cdots & t_{KN}
\end{array}
\right) \\[3pt]
E
&=&
Y-T
\end{eqnarray}
$B$ は同じ列から構成される $K\times N$ 行列である。
式(\ref{pi})の関数 $\pi$ は先に定義したsoftmax関数であり、行列の各成分に作用させることとする。
実装
pythonを使って実装を行なった。
$K=3$、$D=2$、$N=1500$とした。
すなわち、2次元平面上の3分類問題である。1500個の点を3等分し、各集合に1,2,3のラベルを割り振った。
- 8-9行目:式(\ref{softmax})である。
- 12-13行目:式(\ref{eprob})である。
- 16-21行目:式(\ref{update1}),(\ref{update2})である。
- 24-28行目:誤差を描画する関数である。
- 30-45行目:境界線を描画する関数である。
- 47-57行目:観測値を作る関数である。
- 59-64行目:ラベルを作る関数だる。
- 67-104行目:確率的勾配降下法を実行するコードである。
下図は、次式で定義される3つの量を、横軸に試行回数をとり、プロットしたものである。
\begin{eqnarray}
\bar{e}_1&=&\frac{1}{\left|\Lambda\right|}\sum_{n\in\Lambda}\;e_{1n}\;\;(\mbox{赤線})\\
\bar{e}_2&=&\frac{1}{\left|\Lambda\right|}\sum_{n\in\Lambda}\;e_{2n}\;\;(\mbox{緑線})\\
\bar{e}_3&=&\frac{1}{\left|\Lambda\right|}\sum_{n\in\Lambda}\;e_{3n}\;\;(\mbox{青線})\\
\end{eqnarray}
ここで、$\Lambda$ はミニバッチを表し、$|\Lambda|$ はそこに含まれる点の数を表す。

$K=3$の場合、$(W,\vec{b})$ は以下のようになる。
\begin{eqnarray}
W
&=&
\left(\begin{array}{ccc}
w_{11} & w_{12} & w_{13} \\
w_{21} & w_{22} & w_{23}
\end{array}
\right)\\
\nonumber\\[3pt]
\vec{b}
&=&
\left(\begin{array}{c}
b_{1} \\
b_{2} \\
b_{3}
\end{array}
\right)
\end{eqnarray}
また、計算される $\vec{f}$ は次式のようになる。
\begin{eqnarray}
\vec{f}
&=&
\left(\begin{array}{c}
f_{1} \\
f_{2} \\
f_{3}
\end{array}
\right) \\
f_1
&=&
\vec{w}^{\;T}_1\cdot\vec{x}+\vec{b}_1 \\
f_2
&=&
\vec{w}^{\;T}_2\cdot\vec{x}+\vec{b}_2 \\
f_3
&=&
\vec{w}^{\;T}_3\cdot\vec{x}+\vec{b}_3 \\
\vec{w}_1
&=&
\left(\begin{array}{c}
w_{11} \\
w_{21}
\end{array}
\right) \\
\vec{w}_2
&=&
\left(\begin{array}{c}
w_{12} \\
w_{22}
\end{array}
\right) \\
\vec{w}_3
&=&
\left(\begin{array}{c}
w_{13} \\
w_{23}
\end{array}
\right)
\end{eqnarray}
いま、各点集合の境界線を考える。
たとえば、ラベル1を持つ点集合とラベル2を持つ点集合の境界線上では、ラベル1を持つ確率 $p_1$ とラベル2を持つ確率 $p_2$ が等しいはずである。 式(\ref{eprob})より
\begin{eqnarray}
p_1 &=& \frac{\exp{(f_1)}}{\exp{(f_1)}+\exp{(f_2)}+\exp{(f_3)}} \\
p_2 &=& \frac{\exp{(f_2)}}{\exp{(f_1)}+\exp{(f_2)}+\exp{(f_3)}} \\
\end{eqnarray}
であるから、境界線上では、$f_1=f_2$ が成り立つことになる。
従って、この2つの点集合を分ける境界線は次式で記述される。
\begin{equation}
(\vec{w}^{\;T}_1- \vec{w}^{\;T}_2)\cdot\vec{x}+(\vec{b}_1-\vec{b}_2)=0
\end{equation}
同様にラベル2と3を分ける境界線は
\begin{equation}
(\vec{w}^{\;T}_2- \vec{w}^{\;T}_3)\cdot\vec{x}+(\vec{b}_2-\vec{b}_3)=0
\end{equation}
ラベル1と3を分ける境界線は
\begin{equation}
(\vec{w}^{\;T}_1- \vec{w}^{\;T}_3)\cdot\vec{x}+(\vec{b}_1-\vec{b}_3)=0
\end{equation}
である。
これらを図示したものが下図である。ラベル1を持つ点を赤、ラベル2を持つ点を緑、ラベル3を持つ点を青で表している。
青線がラベル1と2の境界線、緑線がラベル2と3の境界線、赤線がラベル1と3の境界線である。

多次元ロジスティック回帰におけるNLLの最小化はconvex optimizationとなるので、初期値に関わらず大域的最小値に収束する。




