計算幾何 〜 記号摂動法 〜

in English

はじめに

　計算幾何アルゴリズムの実装において大切なことは、幾何対象の位相構造を数値計算により正しく判定することである。これを実現するため、数値計算には浮動小数点ではなく十分おおきなビット幅を持つ整数（多倍長整数）を使うべきである。たとえば、入力座標値が浮動小数点ならばその座標値に十分大きな数をかけ、その結果を整数に近似すれば良い。しかし、全く同じ座標値を持つ点（縮退あるいは退化と呼ぶ）が作り出す位相構造の判定は依然として困難である。これを解決するのが記号摂動法と呼ばれる手法である。今回はこの手法について参考書籍をもとに議論したい。

退化

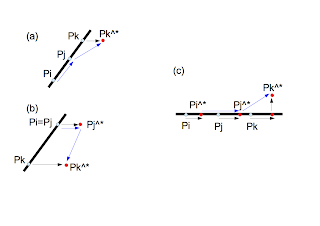
　ここでは、2次元凸包を実装する際に必要となる以下の判定式を取り上げる（2次元凸包についてはこちらで解説した）。 $$\begin{equation} F(P_i,P_j,P_k) = \left| \begin{array}{ccc} 1 & x_i & y_i \\ 1 & x_j & y_j \\ 1 & x_k & y_k \end{array} \right| \end{equation}$$ ここで、$P_i=(x_i,y_i)$、$P_j=(x_j,y_j)$、$P_k=(x_k,y_k)$である。右手系の座標系を考えた場合、上の判定式は次のように使用される。

$P_i \rightarrow P_j \rightarrow P_k$の順にたどったとき、

1. $F(P_i,P_j,P_k) > 0$ならば$P_j$で左に折れる
2. $F(P_i,P_j,P_k) < 0$ならば$P_j$で右に折れる

この判定で問題となる退化とは$F(P_i,P_j,P_k) = 0$の場合である。つまり、$P_i$と$P_j$の作る直線の上に$P_k$が存在する場合である（下図）。

記号摂動法

　点の総数を$n$、考察する3点の添字について$i>j>k$が成立しているとする。 $M$を十分大きな整数、$\epsilon$を十分小さい量とし、各点に摂動を加える。 $$\begin{eqnarray} P_i^{\ast}&=&(x_i+\epsilon^{M^i},y_i+\epsilon^{M^{n+i}}) \nonumber \\ &\equiv&(x_i^{\ast},y_i^{\ast}) \end{eqnarray}$$ $i>j>k$としたから、摂動量は$y_i,y_j,y_k,x_i,x_j,x_k$の順に大きくなる。記号摂動法は以下の手順を踏むことにより退化を解く。

1. 一番摂動量の大きい座標をずらす。いまの場合、$x_k$である。この状態で$P_i \rightarrow P_j \rightarrow P_k$の順にたどり、判定を行う。
2. まだ退化していれば、次に摂動量の大きい座標をずらす。いまの場合、$x_j$である。この状態で$P_i \rightarrow P_j \rightarrow P_k$の順にたどり、判定を行う。
3. 以下同じである。退化が解けるまで続ける。

上の図に摂動を加え、退化を解いたものを以下に示す。摂動を加えた点を赤丸で、退化が解けたときの$P_i \rightarrow P_j \rightarrow P_k$の軌跡を青線で示した。

図の(a)〜(c)に適用される各手順は以下の通りである。

1. $x_k$をずらす。この時点で退化は解ける。
2. $x_k$をずらしても退化は解けない。次に摂動量の大きい$x_j$をずらした時点で退化は解ける。
3. $x$軸に沿って$x_i,x_j,x_k$が存在するから、これらをずらしても退化は解けない。次に摂動量の大きい$y_k$をずらして初めて退化が解ける。

この振る舞いを式で示すため、$F(P^{\ast}_i,P^{\ast}_j,P^{\ast}_k)$を微小量$\epsilon$で展開する。 $$\begin{eqnarray} F(P_i^{\ast},P_j^{\ast},P_k^{\ast}) &=& \left| \begin{array}{ccc} 1 & x_i & y_i \\ 1 & x_j & y_j \\ 1 & x_k & y_k \end{array} \right| \nonumber\\ &&- \left| \begin{array}{ccc} 1 & y_i \\ 1 & y_j \end{array} \right|\;\epsilon^{M^{k}} + \left| \begin{array}{ccc} 1 & y_i \\ 1 & y_k \end{array} \right|\;\epsilon^{M^{j}} - \left| \begin{array}{ccc} 1 & y_j \\ 1 & y_k \end{array} \right|\;\epsilon^{M^{i}}\nonumber\\ &&+ \left| \begin{array}{ccc} 1 & x_i \\ 1 & x_j \end{array} \right|\;\epsilon^{M^{n+k}} - \left| \begin{array}{ccc} 1 & x_i \\ 1 & x_k \end{array} \right|\;\epsilon^{M^{n+j}} + \left| \begin{array}{ccc} 1 & x_j \\ 1 & x_k \end{array} \right|\;\epsilon^{M^{n+i}}\nonumber\\ &&+ \epsilon^{M^{n+k}}(\epsilon^{M^{j}}-\epsilon^{M^{i}}) - \epsilon^{M^{n+j}}(\epsilon^{M^{k}}-\epsilon^{M^{i}}) + \epsilon^{M^{n+i}}(\epsilon^{M^{k}}-\epsilon^{M^{j}}) \label{epsilon_f} \end{eqnarray}$$ 上式は寄与の大きなものから順に並んでいる。(a)〜(c)において退化が解ける様子をこの式を用いて示すことができる。

1. 右辺第1項は0である。第2項（$\epsilon^{M^{k}}$の項）の寄与により退化が解ける。第2項の符号は負であるから$F(P_i^{\ast},P_j^{\ast},P_k^{\ast})<0$となり、$P_j$で右に折れる。
2. 右辺は第2項まで0である。第3項（$\epsilon^{M^{j}}$の項）の寄与により退化が解ける。第3項の符号は負であるから$F(P_i^{\ast},P_j^{\ast},P_k^{\ast})<0$となり、$P_j$で右に折れる。
3. 右辺は第4項まで0である。第5項（$\epsilon^{M^{n+k}}$の項）の寄与により退化が解ける。第5項の符号は正であるから$F(P_i^{\ast},P_j^{\ast},P_k^{\ast})>0$となり、$P_j$で左に折れる。

さらに、3点が重なった場合を考えてみる。

この場合、式($\ref{epsilon_f}$)の第7項までは0である。第8項は$y_k$に対する摂動からの寄与である。$\epsilon^{M^{j}}-\epsilon^{M^{i}}>0$であるから第8項の符号は正である。すなわち、$F(P_i^{\ast},P_j^{\ast},P_k^{\ast})>0$となり、$P_j$で左に折れる。
　以上により、記号摂動法を使えば退化を完全に解くことができることがわかる。

参考文献

計算幾何プログラミング, 杉原厚吉, 岩波書店