いま、観測量$\vec{x}$がラベル$\{c_{k}\},k=1,\cdots,K$のいずれかに属している問題を考える。$\vec{x}$が実現する確率$p(\vec{x})$は
\begin{equation}
p(\vec{x})=\sum_{k=1}^{K} p(\vec{x}, c_{k})
\end{equation}
と書くことができる。ここで、 $p(\vec{x}, c_{k})$は$\vec{x}$と$c_{k}$が同時に実現する確率である。Bayesの定理から上式の右辺は
\begin{equation}
p(\vec{x})=\sum_{k=1}^{K} p(\vec{x}| c_{k})\;p(c_{k})
\label{d0}
\end{equation}
と変形することができる。ここで、$p(\vec{x}| c_{k})$は$c_{k}$が実現しているとき$\vec{x}$が実現する事後確率、$p(c_{k})$は事前確率である。次に、$\vec{x}$が実現しているときラベルが$c_k$である事後確率を考える。Bayesの定理と式($\ref{d0}$)より
\begin{eqnarray}
p(c_k|\vec{x})&=&\frac{p(\vec{x}, c_{k})}{p(\vec{x})} \\
&=&\frac{p(\vec{x}| c_{k})p(c_k)}{\sum_{i} p(\vec{x}| c_{i})\;p(c_{i})} \\
&=&\frac{ {\rm e}^{a_k} }{\sum_{i} {\rm e}^{a_i}} \label{e0}
\end{eqnarray}
を得る。ここで
\begin{eqnarray}
a_k&=&\ln\left(p(\vec{x}| c_{k})p(c_k)\right) \\
&=&\ln p(\vec{x},c_{k})
\end{eqnarray}
とした。式($\ref{e0}$)がSoftmax関数である。先に考えた多次元回帰では、計算の順序として最初に$a_{k}$が計算され、Softmax関数を使って確率に変換していた。$a_{k}$とは$\vec{x}$と$c_k$が同時に実現する確率$p(\vec{x},c_k)$の対数である。
２分類の場合、式($\ref{e0}$)は
\begin{equation}
p(c_1|\vec{x})=\frac{ {\rm e}^{a_1} }{{\rm e}^{a_1}+{\rm e}^{a_2}}
\end{equation}
となる。ここで
\begin{eqnarray}
b&\equiv&a_1-a_2 \\
&=&\ln{\frac{p\left(\vec{x},c_1\right)}{p\left(\vec{x},c_2\right)}}\\
&=&\ln{\frac{p\left(c_1|\vec{x}\right)}{p\left(c_2|\vec{x}\right)}} \label{e1}
\end{eqnarray}
を導入すると
\begin{equation}
p(c_1|\vec{x})=\frac{1}{1+{\rm e}^{-b}}
\end{equation}
を得る。これはシグモイド関数である。先の1次元回帰では最初に$b$を求め、この関数により確率に変換した。
シグモイド関数
\begin{equation}
\sigma=\frac{1}{1+{\rm e}^{-b}}
\end{equation}
を$b$について解いた式
\begin{equation}
b=\ln{\left(\frac{\sigma}{1-\sigma}\right)}
\end{equation}
をlogit関数と呼ぶ。
2016年1月27日水曜日
2016年1月26日火曜日
Softmax関数とシグモイド関数のこと
1次元ロジスティック回帰では以下のシグモイド関数を用いた(参照)。
\begin{equation}
f_{\rm SI}(a)=\frac{1}{1+{\rm e}^{-a}}
\end{equation}
この式により任意の実数$a$は確率に変換される。この回帰の目的は$N$個の多次元ベクトル $\vec{x}_{i},i=1,\cdots,N$ を２分類することである。一方、多次元ロジスティック回帰では、Softmax関数
\begin{equation}
f_{\rm SO}(a_{k})=\frac{{\rm e}^{a_{k}}}{\sum_{i=1}^{M}{\rm e}^{a_{i}}}
\end{equation}
が使われていた(参照)。この回帰の目的は$N$個の多次元ベクトル $\vec{x}_{i},i=1,\cdots,N$ を$M$分類することである。先と同様に、$M$個の実数$a_{k},k=1,\cdots,M$ はこの式により確率に変換されることになる。以下が成り立つ事に注意する。
\begin{equation}
\sum_{k=1}^{M}\;f_{\rm SO}(a_{k})=1
\end{equation}
それでは、$M$が$2$のとき上記のSoftmax関数とシグモイド関数はどのように対応付けられるのであろうか？
$M=2$のとき \begin{equation} f_{\rm SO}(a_{1})=\frac{{\rm e}^{a_{1}}}{{\rm e}^{a_{1}}+{\rm e}^{a_{2}}} \label{eq1} \end{equation} となる。$f_{\rm SO}(a_{2})$は$1-f_{\rm SO}(a_{1})$から求める事ができるので$f_{\rm SO}(a_{1})$だけを考える。式($\ref{eq1}$)変形すると、 \begin{eqnarray} f_{\rm SO}(a_{1})&=&\frac{1}{1+{\rm e}^{-\left(a_{1}-a_{2}\right)}}\\ &=&f_{\rm SI}(a_{1}-a_{2}) \end{eqnarray} を得る。すなわち、２変数の場合はその差だけでSoftmax関数を記述することができる。$a_{1}-a_{2}$を改めて$a$とおけばシグモイド関数に帰着する。$a_1 \gg a_2$は$a$が十分大きいことに対応し、$a_1 \ll a_2$は$a$が十分小さいことに対応する。
$M=2$のとき \begin{equation} f_{\rm SO}(a_{1})=\frac{{\rm e}^{a_{1}}}{{\rm e}^{a_{1}}+{\rm e}^{a_{2}}} \label{eq1} \end{equation} となる。$f_{\rm SO}(a_{2})$は$1-f_{\rm SO}(a_{1})$から求める事ができるので$f_{\rm SO}(a_{1})$だけを考える。式($\ref{eq1}$)変形すると、 \begin{eqnarray} f_{\rm SO}(a_{1})&=&\frac{1}{1+{\rm e}^{-\left(a_{1}-a_{2}\right)}}\\ &=&f_{\rm SI}(a_{1}-a_{2}) \end{eqnarray} を得る。すなわち、２変数の場合はその差だけでSoftmax関数を記述することができる。$a_{1}-a_{2}$を改めて$a$とおけばシグモイド関数に帰着する。$a_1 \gg a_2$は$a$が十分大きいことに対応し、$a_1 \ll a_2$は$a$が十分小さいことに対応する。
2016年1月24日日曜日
2016年1月22日金曜日
Chainerチュートリアルの覚え書き
Chainerのチュートリアルの中程に以下の記述がある。
上記のf.W.gradとf.b.gradを導出する。
計算される量は \begin{equation} Y = WX+B \end{equation} 成分を取ると \begin{equation} y_{i m} = \sum_{j}w_{i j}x_{j m}+b_{i} \end{equation} $w_{\alpha \beta}$で微分を取ると \begin{eqnarray} \frac{\partial y_{i m}}{\partial w_{\alpha \beta}} &=& \sum_{j} \delta_{i \alpha}\delta_{\beta j} x_{j m} \\ &=&\delta_{i \alpha}x_{\beta m} \end{eqnarray} 両辺 $i,m$ で和を取ると \begin{eqnarray} \sum_{im}\frac{\partial y_{im}}{\partial w_{\alpha \beta}} &=& \sum_{im}\delta_{i\alpha}x_{\beta m} \\ &=&\sum_{m}x_{\beta m} \end{eqnarray} この値を $\delta w_{\alpha \beta}$ と置く。 \begin{equation} \delta w_{\alpha \beta}=\sum_{m}x_{\beta m} \end{equation} いま $m=(0,1)$ であるから \begin{equation} \delta w_{\alpha \beta}= x_{\beta 0}+x_{\beta 1} \end{equation} $\beta=(0,1,2)$ であるから \begin{eqnarray} \delta w_{\alpha 0}&=&x_{0 0}+x_{0 1} \\ \delta w_{\alpha 1}&=&x_{1 0}+x_{1 1} \\ \delta w_{\alpha 2}&=&x_{2 0}+x_{2 1} \end{eqnarray} $(x_{0 0},x_{1 0},x_{2 0})=(1,2,3)$, $(x_{0 1},x_{1 1},x_{2 1})=(4,5,6)$ であるから \begin{eqnarray} \delta w_{\alpha 0}&=& 5\\ \delta w_{\alpha 1}&=& 7 \\ \delta w_{\alpha 2}&=& 9 \end{eqnarray} $\alpha=(0,1)$ であることを使えば次式を得る。 \begin{eqnarray} \delta w &=& \begin{pmatrix} \delta w_{00} & \delta w_{01} & \delta w_{02}\\ \delta w_{10} & \delta w_{11} & \delta w_{12} \end{pmatrix} \\ &=& \begin{pmatrix} 5 & 7 & 9\\ 5 & 7 & 9 \end{pmatrix} \end{eqnarray} これが f.W.grad である。次に $b_{j}$ で $y_{im}$ を微分する。 \begin{eqnarray} \delta b_{j} &\equiv& \sum_{im} \frac{\partial y_{im}}{\partial b_{j}}\\ &=&\sum_{im} \delta_{ij} \\ &=&\sum_{m}\\ &=&2 \end{eqnarray} $j=(0,1)$ であるから $(\delta b_{0},\delta b_{1})=(2,2)$ を得る。これが f.b.grad である。
計算される量は \begin{equation} Y = WX+B \end{equation} 成分を取ると \begin{equation} y_{i m} = \sum_{j}w_{i j}x_{j m}+b_{i} \end{equation} $w_{\alpha \beta}$で微分を取ると \begin{eqnarray} \frac{\partial y_{i m}}{\partial w_{\alpha \beta}} &=& \sum_{j} \delta_{i \alpha}\delta_{\beta j} x_{j m} \\ &=&\delta_{i \alpha}x_{\beta m} \end{eqnarray} 両辺 $i,m$ で和を取ると \begin{eqnarray} \sum_{im}\frac{\partial y_{im}}{\partial w_{\alpha \beta}} &=& \sum_{im}\delta_{i\alpha}x_{\beta m} \\ &=&\sum_{m}x_{\beta m} \end{eqnarray} この値を $\delta w_{\alpha \beta}$ と置く。 \begin{equation} \delta w_{\alpha \beta}=\sum_{m}x_{\beta m} \end{equation} いま $m=(0,1)$ であるから \begin{equation} \delta w_{\alpha \beta}= x_{\beta 0}+x_{\beta 1} \end{equation} $\beta=(0,1,2)$ であるから \begin{eqnarray} \delta w_{\alpha 0}&=&x_{0 0}+x_{0 1} \\ \delta w_{\alpha 1}&=&x_{1 0}+x_{1 1} \\ \delta w_{\alpha 2}&=&x_{2 0}+x_{2 1} \end{eqnarray} $(x_{0 0},x_{1 0},x_{2 0})=(1,2,3)$, $(x_{0 1},x_{1 1},x_{2 1})=(4,5,6)$ であるから \begin{eqnarray} \delta w_{\alpha 0}&=& 5\\ \delta w_{\alpha 1}&=& 7 \\ \delta w_{\alpha 2}&=& 9 \end{eqnarray} $\alpha=(0,1)$ であることを使えば次式を得る。 \begin{eqnarray} \delta w &=& \begin{pmatrix} \delta w_{00} & \delta w_{01} & \delta w_{02}\\ \delta w_{10} & \delta w_{11} & \delta w_{12} \end{pmatrix} \\ &=& \begin{pmatrix} 5 & 7 & 9\\ 5 & 7 & 9 \end{pmatrix} \end{eqnarray} これが f.W.grad である。次に $b_{j}$ で $y_{im}$ を微分する。 \begin{eqnarray} \delta b_{j} &\equiv& \sum_{im} \frac{\partial y_{im}}{\partial b_{j}}\\ &=&\sum_{im} \delta_{ij} \\ &=&\sum_{m}\\ &=&2 \end{eqnarray} $j=(0,1)$ であるから $(\delta b_{0},\delta b_{1})=(2,2)$ を得る。これが f.b.grad である。
2016年1月9日土曜日
3D Object Retrieval On SHREC2014 Dataset
Introduction
In the previous page a new method for 3D object retrieval has been evaluated on a 3D object dataset of the SHREC2012 and it has been shown that the five performance metrics, Nearest Neighbor (NN), First-Tier (FT), Second-Tier (ST), F-Measure (F), and Discounted Cumulative Gain (DCG), are all better than those by the other studies shown in the page. In this page the same method is applied to the dataset of the SHREC2014 and it is again demonstrated that the five metrics are higher than the other studies.
Dataset
The SHREC2014 dataset consists of 171 categories each of which has 3D models that are in the ASCII Object File Format (*.off). The total number of the 3D models is 8987. In order to train the CNN, a set of 3D models in each category is divided by the split ratio 4:1. The former group corresponds to a training dataset in which the number of 3D models is 7123. The latter one includes 1864 3D models and is considered as a testing dataset. As explained here, in the proposed method 20 gray images are created per 3D model and the category of the corresponding 3D model is assigned to those 20 images. Therefore, the numbers of the training and the testing images are 142460(=20$\times$7123) and 37280(=20$\times$1864), respectively.
| the number of training images | the number of testing images |
|---|---|
| 142460 | 37280 |
Definition of Network
The CNN model (bvlc_alexnet/bvlc_alexnet.caffemodel) that Caffe provides is fine-tuned on the training dataset. The detailed information on the fine-tuning procedures is described in this page. The prototxt file used for training is as follows: The solver file is as follows: This script is run in order to train the CNN. The fine-tuning process is shown below.
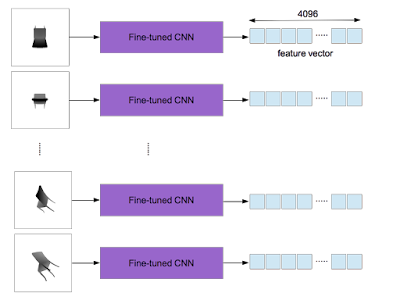
After training, an output of the layer "fc7" is used as a feature vector (4096 dimensions). In the proposed method a 3D object yields 20 gray images which are converted from depth ones. The fine-tuned CNN used as the feature extractor is applied to each of them and 20 feature vectors are obtained per 3D object.
According to the work by H. Su et al., the element-wise maximum operation across the 20 vectors is used to make a single feature vector with 4096 dimensions as shown below.
Evaluation On SHREC2014
Now that the feature extractor is constructed, five standard performance metrics, Nearest Neighbor (NN), First-Tier (FT), Second-Tier (ST), F-Measure (F), and Discounted Cumulative Gain (DCG), can be calculated by means of three evaluation programs:
- SHREC2014_Comprehensive_Evaluation.m
- SHREC2014_Comprehensive_Evaluation_Proportional_Weight.m
- SHREC2014_Comprehensive_Evaluation_Reciprocal_Weight.m
Performance metrics:
| NN | FT | ST | F | DCG | |
|---|---|---|---|---|---|
| my result | 0.904 | 0.569 | 0.683 | 0.275 | 0.849 |
| the previous best result | 0.868 | 0.528 | 0.661 | 0.255 | 0.823 |
Proportional Weighted Performance metrics:
| NN | FT | ST | F | DCG | |
|---|---|---|---|---|---|
| my result | 188.087 | 123.136 | 149.292 | 37.709 | 179.756 |
| the previous best result | 178.981 | 107.851 | 144.179 | 33.691 | 173.773 |
Reciprocally Weighted Performance metrics:
| NN | FT | ST | F | DCG | |
|---|---|---|---|---|---|
| my result | 5.025 | 3.061 | 3.595 | 1.820 | 4.626 |
| the previous best result | 4.881 | 2.905 | 3.435 | 1.731 | 4.470 |
登録:
投稿 (Atom)