word2vec その2

はじめに

　このページの続きです。

やりたいこと

　単語列 $$\begin{equation} W = \{w_1,\cdots, w_T\} \end{equation}$$ が与えられているとき、この単語列に含まれる任意の単語$w_t$を考える。$w_t$を含む文からその周辺の単語の集合$\Xi_{w_t}$を作ることができる。 $$\begin{equation} \Xi_{w_t} = \{\xi_1^t, \cdots, \xi_C^t\} \end{equation}$$ このとき、以下の対数尤度を考える。 $$\begin{eqnarray} L&=&\sum_{t=1}^T \sum_{c=1}^{C} \biggl\{ \log{\sigma(s(\xi_c^t,w_t))}+\sum_{w \in {\rm Ng}}\log{\sigma(-s(w,w_t))} \biggr\} \label{obj}\\ \sigma(x) &=& \frac{1}{1+\exp{(-x)}}\\ s(a,b) &=& \vec{u}^T_a \cdot \vec{v}_b \end{eqnarray}$$ ここで、${\rm Ng}$は分布 $$\begin{equation} p(w) = \frac{U(w)^{0.75}}{\sum_{t=1}^{T}U(w_t)^{0.75}} \end{equation}$$ に従ってサンプリングした$k$個の単語の集合である。$U(w)$は単語の出現頻度である。本ページでは、上記の対数尤度の最大化問題を、Neural Networkを用いて解くことができることを示す。

Neural Networkによる表現

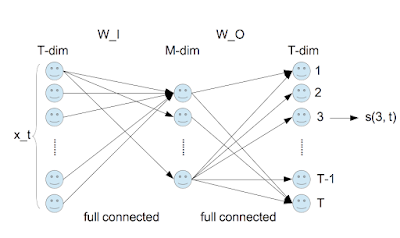
　単語列$W$内の$t$番目の単語$w_t$を以下のone-hot vector $\vec{x}_t$で表現する。 $$\begin{equation} \vec{x}_t = \left( \begin{array}{c} 0 \\ \vdots \\ 1 \\ 0 \\ \vdots \\ 0 \end{array} \right) \end{equation}$$ $t$番目の要素だけが1の$T$次元ベクトルである。次に、行列$W_I$と$W_O$を次式で定義する。 $$\begin{eqnarray} W_I&=&\left[\vec{v}_1, \cdots, \vec{v}_T\right] \\ W_O&=&\left( \begin{array}{c} \vec{u}_1^T \\ \vdots \\ \vec{u}_T^T \end{array} \right) \end{eqnarray}$$ ここで、$\vec{v}_t$と$\vec{u}_t$は$M$次元ベクトルとする。従って、$W_I$は$M\times T$行列、$W_O$は$T\times M$行列である。これらを用いると $$\begin{eqnarray} (W_O\; W_I\; \vec{x}_t)_i &=& (W_O)_{ik}\;(W_I\;\vec{x}_t)_k \\ &=&(W_O)_{ik}\;(W_I)_{km} (\vec{x}_t)_{m}\\ &=& u_{ik}\;v_{mk}\;x_{tm} \\ &=& u_{ik}\;v_{mk}\;\delta_{tm} \\ &=& u_{ik}\;v_{tk} \\ &=& \vec{u}_{i}^T \cdot \vec{v}_{t} \\ &=& s(i, t) \end{eqnarray}$$ となる。これを図にすると以下のようなる。

以上から以下のことが分る。

1. 式($\ref{obj}$)の第1項に含まれる$s(\xi_c^t, w_t)$を計算するには、$w_t$に相当するone-hot vector $\vec{x}_t$をネットワークに入力し、その出力ベクトル（$T$次元ペクトル）の成分のうち、$\xi_c^t$に相当するものを取り出せば良い。
2. 式($\ref{obj}$)の第2項に含まれる$s(w, w_t)$の計算も同様である。

これらの計算のあと活性化関数としてsigmoid関数を作用させ、従来の手法（確率的最急降下法など）を使って$L$を最適化すれば良い。この計算で求まる行列$W_I$を使って単語$w_t$を表現するベクトル$\vec{v}_t$が次式で決まる。 $$\begin{equation} \vec{v}_t = W_I\;\vec{x}_t \end{equation}$$ $T \gg M$と取るので低次元で効率良く単語を表現できるベクトルを得ることができる。

Chainerによる実装

　Chainerのソースには、word2vecのサンプルプログラムが含まれている。このサンプルプログラムには、Skip Gram以外にContinuous BoWも実装されており、さらに、Negative Sampling以外の損失関数も選択できるようになっている。以下に示すのは、サンプルプログラムを参考にして、Skip GramかつNegative Samplingの場合のクラスを実装したものである。

1. 5行目で定義されるL.EmbedIDは、$W_I$に相当する。
2. 6行目で定義されるL.NegativeSamplingは、式($\ref{obj}$)を計算する。この関数の中に$W_O$に相当するものがある。
3. n_vocabは$T$、n_unitsは$M$に相当する。
4. countsは$U(w)$に相当する。
5. sample_sizeは$k$に相当する。
6. 13行目の引数xはいま対象にする単語$w_t$、contextは$\Xi_{w_t}$に相当する。ただし、batch処理が考慮されている。

ここまでは式と対応付けることができたが、関数__call__の中で行っている処理で分らなくなる。最初にself.embed(context)を実行している。$\Xi_{w_t}$の中の1つの単語を$\vec{x}_t$とおくと、この計算は$W_I\;\vec{x}_t$に相当してしまう。定式化では$\Xi_{w_t}$に含まれる単語には$W_O$が作用するはずである。さてどこでおかしくなったのか？

word2vec その1

はじめに

　word2vecについてまとめます（その2を書きました）。

やりたいこと

　ある程度まとまった量の文章$A$を考える。これに出現する単語を重複を許さずに取り出すと、長さ$T$の単語列が出来上がる。 $$\begin{equation} W = \{w_1, \cdots, w_T\} \end{equation}$$ いま、この単語列に含まれる単語$w_t$を含む文を$A$から取り出し、$w_t$の前後$b$個の範囲にある単語の集合$\Xi_{w_t}$を考える。 $$\begin{equation} \Xi_{w_t} = \{\xi_1^t, \cdots, \xi_C^t\} \end{equation}$$ これは文脈を反映した集合である。たとえば、

Linux was originally developed as a free operating system for personal computers based on the Intel x86 architecture.

という文からは、$w_t={\rm developed}$、$b=1$のとき $$\begin{equation} \Xi_{{\rm developed}} = \{{\rm originally}, {\rm as}\} \end{equation}$$ を、$w_t={\rm free}$のとき $$\begin{equation} \Xi_{{\rm free}} = \{{\rm a}, {\rm operating}\} \end{equation}$$ を得る。$w_t$を指定したとき$\Xi_{w_t}$が実現する確率 $$\begin{equation} p(\Xi_{w_t}|w_t) \end{equation}$$ を最大化するような単語の表現（ベクトル）を求めることがword2vec（Skip-Gram model）の目的である。

対数尤度の最大化

$$\begin{eqnarray} p(\Xi_t|w_t) &=& p(\xi_1^t, \cdots, \xi_C^t|w_t) \\ &=& \prod_{c=1}^{C}p(\xi_c^t|w_t) \end{eqnarray}$$ 対数をとり、全ての単語について足し合わせたもの $$\begin{equation} L=\sum_{t=1}^T \sum_{c=1}^{C}\log{p(\xi_c^t|w_t)} \label{obj} \end{equation}$$ を最大化する。

Softmax関数による計算

　$p(\xi_c^t|w_t)$としてSoftmax関数を仮定する。 $$\begin{equation} p(\xi_c^t|w_t)=\frac{\exp{\vec{u}^T_{\xi_c^{\;t}} \cdot \vec{v}_{w_t}}}{\sum_{w \in W} \exp{\vec{u}^T_w \cdot \vec{v}_{w_t}}} \end{equation}$$ ここで、$\vec{v}$は入力単語を表現するベクトル、$\vec{u}$は出力単語を表現するベクトルである。$\sum_{w \in W}$は全単語について足し合わすことを意味する。モデルに入力する単語とモデルが出力する単語は区別されることに注意する。式($\ref{obj}$)に代入すると $$\begin{equation} L = \sum_{t=1}^T \sum_{c=1}^{C} \left\{ s(\xi_c^t, w_t) - \log{\sum_{w \in W} \exp{s(w, w_t)}} \right\} \end{equation}$$ を得る。ただし、$s(a,b) = \vec{u}^T_a \cdot \vec{v}_b$とした。$W$の要素数が少なければ総和（$\sum_{w \in W}$）を取ることは可能であるが、現実の問題では$10^5\sim10^7$のオーダーであるため計算は困難である。

1次元ロジスティック回帰による計算（2分類問題への置き換え）

　単語$a$と$b$が与えられたとき、これらが同じ文脈上に存在する確率を$p(D=1|a, b)$、同じ文脈上に存在しない確率を$p(D=0|a, b)$とする。 このとき、次式のように書くことができる。 $$\begin{equation} p(D|a,b)=p(D=1|a, b)^{D}\; p(D=0|a, b)^{1-D} \end{equation}$$ ここで以下を考える。

1. $w_t$が与えられた時の集合$\Xi_{w_t}$の各要素は、$w_t$と同じ文脈上に存在する。
2. $w_t$が与えられた時の集合$\Xi_{w_t}$に属さない要素は、$w_t$と同じ文脈上に存在しない。

これらを実現するには、次の対数尤度を最大化すればよい。 $$\begin{equation} L = \sum_{t=1}^T \sum_{c=1}^{C} \biggl\{ D_t \log{p(D_t=1|\xi^t_c, w_t)}+\sum_{w \not\in \Xi_{w_t}}(1-D_t)\log{p(D_t=0|w, w_t)} \biggr\} \label{f1} \end{equation}$$ さらに $$\begin{eqnarray} p(D_t=1|a, b) &=& \sigma(s(a,b)) \\ p(D_t=0|a, b) &=& 1- \sigma(s(a,b)) = \sigma(-s(a,b)) \end{eqnarray}$$ を仮定すれば（$\sigma(x)$はシグモイド関数）、1次元ロジスティック回帰の問題に帰着する。 式($\ref{f1}$)を最大にすることにより

1. 同じ文脈上にある2語の確率を高くし（第1項からの寄与）
2. 同じ文脈上にない2語の確率を高くする（第2項からの寄与）

ことが実現される。上記とほとんど同じことであるが次式を最大化する手法が存在する。 $$\begin{equation} L = \sum_{t=1}^T \sum_{c=1}^{C} \biggl\{ \log{p(D_t=1|\xi^t_c, w_t)}+\sum_{w \in {\rm Ng}}\log{p(D_t=0|w, w_t)} \biggr\} \end{equation}$$ ${\rm Ng}$は、分布 $$\begin{equation} p(w) = \frac{U(w)^{0.75}}{\sum_{t=1}^{T}U(w_t)^{0.75}} \end{equation}$$ に従ってサンプリングした$k$個の単語の集合である。$U(w)$は単語の頻度である。人為的に外れ(negative)データを導入することから、本手法をNegative Samplingと呼ぶ（その2を書きました）。