論文読み「Your Classifier Is Secretly An Energy Based Model And You Should Treat It Like One」

はじめに

　「Your Classifier Is Secretly An Energy Based Model And You Should Treat It Like One」をまとめる。

概要

同時分布$p({\bf x},y)$をEnergy Based Modelで表すことにより、従来の識別器（discriminative classifier：$p(y|{\bf x})$）から$p({\bf x},y)$を導出することができる。

$p({\bf x})$も容易に求めることができる。

従来の手順で求められる識別器が出発点となる。ラベル付けされていないデータを用いて訓練される。

本手法を用いて同時分布$p({\bf x},y)$を訓練することにより、較正度合い、敵対的サンプルに対する頑健さ、分布外検知を改善することができる。それと同時に、最近のGANに匹敵する高画質画像を生成することができる。

Energy Based Modelの訓練を大規模に行うテクニックを改善し、通常の識別器の訓練とほとんど同じオーバヘッドで行う手法を与える。

Energy Based Model

　パラメータ$\theta$を持つ同時確率分布$p_{\theta}({\bf x},y)$をボルツマン分布を用いて表す。 \begin{equation} p_{\theta}({\bf x},y)=\frac{\exp{ \left( -E_{\theta} ({\bf x},y) \right) } }{Z(\theta)} \label{eq1} \end{equation} $E_{\theta}({\bf x},y)$はエネルギーであり、その定義については後述する。$Z(\theta)$は次式で定義される分配関数である。 \begin{equation} Z(\theta)=\int dx\int dy \exp{ \left( -E_{\theta} ({\bf x},y) \right) } \label{eq2} \end{equation} 式(\ref{eq1})のように確率分布をボルツマン分布を用いて表すモデルを、Energy Based Modelと呼ぶ。式(\ref{eq1})を$y$について周辺化して \begin{equation} p_{\theta}({\bf x}) = \int dy\;p_{\theta}({\bf x},y) \label{eq3} \end{equation} を得る。いま、$p_{\theta}({\bf x})$に対してもボルツマン分布を仮定する。 \begin{equation} p_{\theta}({\bf x})=\frac{\exp{\left(-E_{\theta}({\bf x})\right)}}{Z(\theta)} \label{eq5} \end{equation} これを変形すると \begin{eqnarray} \exp{\left(-E_{\theta}({\bf x})\right)} &=& Z(\theta)p_{\theta}({\bf x})\nonumber\\ &=& Z(\theta) \int dy\;p_{\theta}({\bf x},y)\nonumber\\ &=& Z(\theta) \int dy \frac{\exp{ \left( -E_{\theta} ({\bf x},y) \right) }}{Z(\theta)}\nonumber\\ &=& \int dy \exp{ \left( -E_{\theta} ({\bf x},y) \right) } \label{eq6} \end{eqnarray} 両辺の対数を取り \begin{equation} E_{\theta}({\bf x})=-\ln{\left( \int dy \exp{ \left( -E_{\theta} ({\bf x},y) \right) } \right) } \label{eq7} \end{equation} を得る。ここまでの手順をまとめると以下のようになる。

1. エネルギー$E_{\theta}({\bf x},y)$を与える。
2. 式(\ref{eq1})から$p_{\theta}({\bf x},y)$を計算する。
3. 式(\ref{eq7})から$E_{\theta}({\bf x})$を計算する。
4. 式(\ref{eq5})から$p_{\theta}({\bf x})$を計算する。

つまり、エネルギー$E_{\theta}({\bf x},y)$が決まれば、さまざまな量を求めることができる。

エネルギーの定義

　$E_{\theta}({\bf x},y)$について考えるため、従来の識別器の構成を示す（下の左図）。

Softmaxに入る前の出力を$f_{\theta}({\bf x})$と書くと、Softmaxによる出力が従来の識別器$p_{\theta}(y|{\bf x})$に相当する。 \begin{equation} p_{\theta}(y|{\bf x}) = \frac { \exp{\left(f_{\theta}({\bf x})[y] \right)} } { \sum_{y^{\prime}}\exp{\left(f_{\theta}({\bf x})[y^{\prime}] \right)} } \end{equation} ここで、$f_{\theta}({\bf x})[y]$は$f_{\theta}({\bf x})$の$y$番目の成分である。本文献では次式によりエネルギーを定義する。 \begin{equation} E_{\theta}({\bf x},y)=-f_{\theta}({\bf x})[y] \end{equation} 上の右側の図は、出力$f_{\theta}({\bf x})$から$p_{\theta}({\bf x},y)$や$p_{\theta}({\bf x})$が導出される様子を示している。本文献の手法をJoint Energy Model（JEM）と呼ぶ。

最適化

　学習時に最大化する目的関数は次式である。 \begin{equation} \ln{p_{\theta}({\bf x},y)}=\ln{p_{\theta}({\bf x})}+\ln{p_{\theta}(y|{\bf x})} \label{eq9} \end{equation} 第2項の最大化は従来とおりクロスエントロピーを用いれば良い。第1項の最大化については以下のようにする。最初に、式(\ref{eq5})の両辺の対数をとる。 \begin{equation} \ln{p_{\theta}({\bf x})}=-E_{\theta}({\bf x})-\ln{Z(\theta)} \end{equation} $\theta$で微分すると \begin{equation} \frac{\partial\ln{p_{\theta}({\bf x})}}{\partial\theta}=-\frac{\partial E_{\theta}({\bf x})}{\partial\theta} -\frac{1}{Z(\theta)}\frac{\partial Z(\theta)}{\partial\theta} \end{equation} ここで \begin{equation} Z(\theta)=\int dx \exp{\left(-E_{\theta}({\bf x})\right)} \end{equation} であるから、これを$\theta$で微分すると \begin{equation} \frac{\partial Z(\theta)}{\partial\theta}=\int dx \exp{\left(-E_{\theta}({\bf x})\right)}\left(-\frac{\partial E_{\theta}({\bf x})}{\partial\theta}\right) \end{equation} 故に \begin{eqnarray} \frac{1}{Z(\theta)}\frac{\partial Z(\theta)}{\partial\theta} &=& -\int dx \frac{\exp{\left(-E_{\theta}({\bf x})\right)}}{Z(\theta)} \left(\frac{\partial E_{\theta}({\bf x})}{\partial\theta}\right)\nonumber\\ &=& -\int dx p_{\theta}({\bf x}) \left(\frac{\partial E_{\theta}({\bf x})}{\partial\theta}\right)\nonumber\\ &=&-\mathbb{E}_{ p_{\theta}({\bf x}) } \left[ \frac{\partial E_{\theta}({\bf x})}{\partial\theta} \right] \end{eqnarray} となる。最後の等式は$p_{\theta}({\bf x})$による期待値であることを表す。以上から \begin{equation} \frac{\partial\ln{p_{\theta}({\bf x})}}{\partial\theta}=-\frac{\partial E_{\theta}({\bf x})}{\partial\theta} +\mathbb{E}_{ p_{\theta}({\bf x}) } \left[ \frac{\partial E_{\theta}({\bf x})}{\partial\theta} \right] \end{equation} を得る。$E_{\theta}({\bf x})$は式(\ref{eq7})により計算することができる。上式の第2項は分布$p_{\theta}({\bf x})$からサンプリングする必要がある。 本文献で使用するサンプリング手法は以下の通りである。 \begin{eqnarray} {\bf x}_{0}&\sim&p_0({\bf x}) \nonumber\\ {\bf x}_{i+1}&=&{\bf x}_i-\frac{\alpha}{2}\frac{\partial E_{\theta}({\bf x}_i)}{\partial {\bf x}_i}+\epsilon\nonumber\\ \epsilon&\sim&\mathcal{N}(0,\alpha) \end{eqnarray} ここで、$p_0({\bf x})$は一様分布である。本手法は、Stochastic Gradient Langevin Dynamics（SGLD）をベースにしたものである（詳細は略）。式(\ref{eq9})の第1項は教師なし学習、第2項は教師あり学習を行う。

実験

識別モデル、生成モデルのどちらに対しても、現在SOTAとされている手法に匹敵する性能を実現した。

識別モデルにおいて、不確かさ評価（uncertainty quantification）、分布外検知、敵対的サンプル（adversarial example）に対する頑健さ、が改善された。　

本文献で用いるネットワークは、Wide Residaul Networkである。このネットワークから$f_{\theta}({\bf x})$を取り出す。

データセットCIFAR10を用いてハイパーパラメータを調節した。本文献で検証するモデルは全て同じハイパーパラメータを用いた。

SGLDサンプラーで使うパラメータは、本文献で扱うデータセットやモデルアーキテクチャの全てで共有できた。

訓練時間は、1つのGPUで36時間ほどであった。

Hybrid Modelint

　従来手法と比較したのが下図である。使用したデータセットは、CIFAR10である。

Class欄に「Hybrid」とあるのが、識別モデルと生成モデルを同時に構築する手法（本手法JEMも含まれる）、「Disc.」欄、「Gen.」欄にあるのが　それぞれ識別モデルだけ、生成モデルだけの手法である。IS（Inception Score）は大きいほど、FID（Frechet Inception Distance）は小さいほど良い指標である。FID以外はJEMが優位であることが分かる。 上の表の4行目にある「JEM$p({\bf x}|y)$ factored」は式(\ref{eq9})の代わりに次式を最大化した結果である。 \begin{equation} \ln{p_{\theta}({\bf x},y)}=\ln{p_{\theta}(y)}+\ln{p_{\theta}({\bf x}|y)} \end{equation} このとき、精度が大きく落ちることが分かる。　

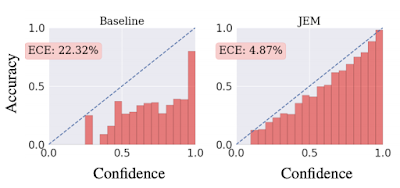
Calibration

　較正済み識別器（calibrated classifier）とは、$\max_y{p(y|{\bf x})}$（確信度）が正解率（accuracy）と比例するような識別器のことである。高い確信度を持って予測されたラベルは高い確率で正解となり、低い確信度で予測されたラベルは、誤認識である確率が高くなる。較正されているか否かを可視化する手順は以下の通り。

1. データセット内の各サンプル${\bf x}_i$ごとに$\max_y{p(y|{\bf x}_i)}$を算出し、これらを等区間のバケットに振り分ける（ヒストグラムを作る）。例えば0から1までの区間を20等分した場合、20個のバケットに振り分ける。
2. 各バケットに属するサンプルから平均精度を算出し、このバケットの高さとする。

上の手順を経ると以下のような図を得る。

上の右図のように確信度と精度が比例するとき、識別器は良く較正されているとみなすことできる。左図は従来手法で訓練した識別器による結果、右図はJEMで訓練した識別器による結果である。全サンプルを用いて算出した精度は、前者が74.2%、後者が72.2%であり、較正された識別器の方が悪い。従って、較正の良し悪しと精度の良さは一致するとは限らないことに注意しなければならない。実環境で有用とされる識別器は、較正されたものである。
　較正度合いを定量化する指標が、次式で定義されるExpected Calibration Error（ECE）である。 \begin{equation} {\rm ECE}=\sum_{m=1}^{M}\frac{|B_m|}{n}|{\rm acc}(B_m)-{\rm conf}(B_m)| \end{equation} ここで、$M$はバケットの数、$n$はデータセット内のサンプル総数、$B_m$は１つののバケット中に格納されるサンプルの集合、$|B_m|$はサンプル数、${\rm acc}(B_m)$は集合$B_m$を用いて計算された平均精度、${\rm conf}(B_m)$は集合$B_m$を用いて計算された平均確信度である。${\rm ECE}$が小さくなるほど較正度合いは良くなり、完全に較正されている場合は0になる。上図に見るように、従来手法による識別器より、JEMで訓練した識別器の方が${\rm ECE}$は小さい。

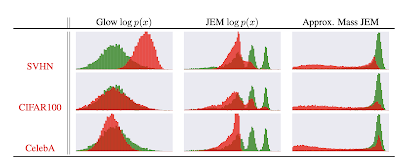
Out-Of-Distribution Detection

　分布外検知とは例えば以下のような識別器を作ることである（引用元）。

猫の画像が与えられる。この画像で訓練する（教師なし学習）。出来上がった識別器に猫の画像を与えると正常（in-distribution）を、フクロウを撮影した画像を与えると異常（out-of-distribution）を返す。

犬・鳥の2種類の画像で訓練し識別器を作る（教師あり学習）。出来上がった識別器に犬・鳥の画像を与えると正常を、馬の画像を与えると異常を返す。

　データセットCIFAR10で訓練した識別器に別の3つのデータセットSVHN、CIFAR100、CelebAを与えときのサンプルの対数分布（$\ln{p(x)}$）を示したのが下図である。

緑の分布がCIFAR10の分布、赤の分布が他のデータセットの分布を表す。「Glow $\log{p(x)}$」の列はGlowと呼ばれる手法による結果、「JEM $\log{p(x)}$」の列にある結果がJEMによるものである。赤い分布と緑の分布が良く分離できているのは後者の方である。

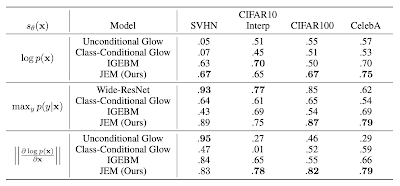
　分布外検知に成功している多くの手法が採用している指標が次式である。 \begin{equation} s_{\theta}({\bf x})=\max_y{p_{\theta}(y|{\bf x})} \end{equation}

表の真ん中の行は上の指標で各種手法を比較したものである。CIFAR10で訓練した場合、データセットSVHNとInterpのサンプルを分布外であると一番良く認識できているのはWide-ResNetである。一方、CIFAR100とCelebAをサンプルとして与えたときは、JEMの認識が一番良い。

Robustness

　JEMは敵対的サンプルに対しても頑健であると主張されている（詳細は略）。

まとめ

同時分布$p({\bf x},y)$をEnergy Based Modelで表すことにより、従来の識別器（discriminative classifier：$p(y|{\bf x})$）から$p({\bf x},y)$を導出することができる。

$p({\bf x})$も容易に求めることができる。

従来の手順で求められる識別器が出発点となる。ラベル付けされていないデータを用いて訓練される。

本手法を用いて同時分布$p({\bf x},y)$を訓練することにより、較正度合い、敵対的サンプルに対する頑健さ、分布外検知を改善することができる。それと同時に、最近のGANに匹敵する高画質画像を生成することができる。

Energy Based Modelの訓練を大規模に行うテクニックを改善し、通常の識別器の訓練とほとんど同じオーバヘッドで行う手法を与える。