Mean Shift Filteringの理論と実践

in English

はじめに

　前回、Mean Shift の理論をまとめました。今回は、D. Comaniciu と P. Meer により提案された Mean Shift Filtering についてまとめます。

理論

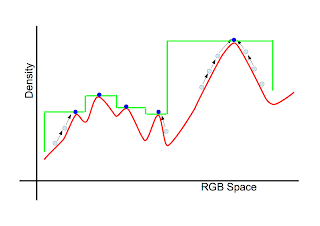
　$n$ 個の画素から構成される $RGB$ 画像を考える。各画素は $(r,g,b)$ を持つ。3次元空間内の点の分布を考えれば、前回と同様に密度分布関数を定義することができる。点が疎らに存在する領域の密度は低く、点が密に存在する領域の密度は高い。いま、Mean Shiftを用いて密度分布関数の極大値を検出していくと図のようになるであろう（青丸で極大値を表した）。

$RGB$ 空間内の任意の3次元ベクトル $\vec{x}$ は、図に見るように、その近傍にある極大値に向かって収束していく。画像内の全ベクトル（全画素）を、それらが収束する極大値の色に置き換えれば、色の平滑化を行うことができる（平滑化後の密度分布関数を緑の線で示した）。

　画像は色だけでなく位置の情報も含む。上記の方法は位置を無視しているので、離れた場所にあるオブジェクト $A$ と $B$ が、たまたま類似色であったため、同じ色（同じラベル）に収束してしまうことがある。オブジェクト $A$ と $B$ に異なるラベルを割り振りたい場合、これでは都合が悪い。そこで、D. Comaniciu と P. Meer は、各画素を表現するベクトルを $(r,g,b)$ ではなく位置情報を含む5次元ベクトル $(x,y,r,g,b)$ に拡張することを考えた^1,2。このとき、Mean Shiftで使用するカーネルは以下のように変更される。 $$\begin{equation} K(\vec{x}_i;\;\vec{x},h)=K_{\rm spatial}(\vec{x}_i^{\;s};\;\vec{x}^{\;s},h_s)\;K_{\rm range}(\vec{x}_i^{\;r};\;\vec{x}^{\;r},h_r) \end{equation}$$ ここで、$\vec{x}=(\vec{x}^{\;s},\vec{x}^{\;r})$、$\vec{x}^{\;s}=(x,y)$、$\vec{x}^{\;r}=(r,g,b)$、$h_s$ は位置空間内の球の半径、$h_r$ は色空間内の球の半径である。このカーネルを使い、次式で重心を計算する。 $$\begin{equation} \vec{m}(\vec{x}) = \frac{\sum_{i=1}^{n}\;K(\vec{x}_i;\;\vec{x},h)\;\vec{x}_i}{\sum_{i=1}^{n}\;K(\vec{x}_i;\;\vec{x},h)} \end{equation}$$ $\vec{x}^{\;s}$ と $\vec{x}^{\;r}$ の区別がなされるのはカーネル計算時のみである。あとの計算はこれまでと同じである。Mean Shiftの手順を画像内の全ての点 $\{\vec{x}_{i}|i=1,\cdots,n\}$ に適用すると、収束点の集合 $\{\vec{z}_{i}|i=1,\cdots,n\}$ を得る。元の点の色成分 $\vec{x}_i^{\;r}$ を、収束点の色成分 $\vec{z}_i^{\;r}$ に置き換えることにより、新たな点 $\vec{y}_i=(\vec{x}_i^{\;s},\vec{z}_i^{\;r})$ を作る。集合 $\{\vec{y}_{i}|i=1,\cdots,n\}$ から構成される画像が求める結果である。

OpenCVによる実践

cv::pyrMeanShiftFilteringを使えば良い。実装例は以下の通り。 14行目でcv::pyrMeanShiftFilteringを呼び出している。第1引数が入力画像、第2引数が出力画像である。第3引数と第4引数はそれぞれ、$h_{s}$と$h_{r}$に相当する。第6引数はアルゴリズムの停止条件である。ピラミッド画像を利用する場合は第5引数にその階層数を指定する。今回は現画像に一度だけ適用したいので0とした。結果は以下の通りである。
元画像：

$(h_s,h_r)=(16,32)$:

$(h_s,h_r)=(16,64)$:

両者ともparams.max_iteration_count_=30, params.epsilon_=0.01とした。ソースを見ていないのでcv::pyrMeanShiftFilteringの内部で使われているカーネルの具体的な形は分りません。たぶん福永カーネルかな？

参考文献

1. Mean Shift Analysis and Applications, D. Comaniciu and P. Meer, 1999 (pdf)
2. Mean Shift: A Robust Approach Toward Feature Space Analysis, D. Comaniciu and P. Meer, 2002 (pdf)
3. コンピュータビジョン2 最先端ガイド　第2章, アドコム・メディア株式会社