3D Object Retrieval On SHREC2012 Dataset

Introduction

　In the previous page a new method for 3D object recognition which is based on the work by H. Su et al. is proposed and evaluated on two 3D object datasets of the ModelNet10 and the ModelNet40. The classification accuracies for them reach 92.84% and 90.92%, respectively. The method employs a convolutional neural network (CNN) as a feature extractor and a support vector machine (SVM) as a classifier. In this page 3D object retrieval on SHREC2012 dataset is performed using the feature extractor which is the part of the new method. It is demonstrated that Nearest Neighbor (NN), First-Tier (FT), Second-Tier (ST), F-Measure (F), and Discounted Cumulative Gain (DCG) are all better than those by the other studies shown in the page.

Dataset

　The SHREC2012 dataset consists of 60 categories each of which has 20 3D models that are in the ASCII Object File Format (*.off). The total number of the 3D models is 1200. In order to train the CNN, a set of 3D models in each category is divided by the split ratio 4:1. The former group corresponds to a training dataset in which the number of 3D models is 960. The latter one includes 240 3D models and is considered as a testing dataset. As explained here, in the proposed method 20 gray images are created per 3D object. Therefore, the numbers of the training and the testing images are 19200(=20$\times$960) and 4800(=20$\times$240), respectively. Since the vertical and the horizontal flipped images are added only to the training dataset, its number is finally 57600(=3$\times$19200).

the number of training images	the number of testing images
57600	4800

Algorithm

　The CNN model (bvlc_reference_caffenet.caffemodel) that Caffe provides is fine-tuned on the training dataset. The detailed information on the fine-tuning procedures is described in this page. The following figure shows a fine-tuning process.

The x-axis indicates the iteration number and the y-axis the recognition accuracy. Because in my work the total iteration number is set to 59,000 and a solver file, where parameters for training are defined, is designed to output the accuracy once per 1000 iterations, the maximum value of the x-axis is 59(=59,000/1000). It can be seen that the recognition accuracy reaches about 78.9%.
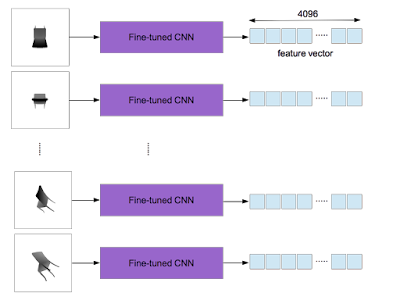
　After training, an output of the layer "fc7" is used as a feature vector (4096 dimensions). As explained here, in the proposed method a 3D object yields 20 gray images which are converted from depth ones. The fine-tuned CNN used as the feature extractor is applied to each of them and 20 feature vectors are obtained per 3D object.

According to the work by H. Su et al., the element-wise maximum operation across the 20 vectors is used to make a single feature vector with 4096 dimensions as shown below.

It is worthy of noting that one feature vector per 3D object is obtained.

Evaluation Measures

　Now that the feature extractor is constructed, five standard performance metrics, Nearest Neighbor (NN), First-Tier (FT), Second-Tier (ST), F-Measure (F), and Discounted Cumulative Gain (DCG), can be calculated by means of the evaluation code, SHREC2012_Generic_Evaluation.m, which is an m-file for MATLAB. The tables shown below compare the proposed method and the other studies. The latter results are quoted from the page.

Nearest Neighbor (NN)

Method	NN
LSD-sum	0.517
ZFDR	0.818
3DSP_L3_200_hik	0.708
DVD+DB	0.831
DG1SIFT	0.879
the proposed method	0.943

First-Tier (FT)

Method	FT
LSD-sum	0.232
ZFDR	0.491
3DSP_L2_1000_hik	0.376
DVD+DB+GMR	0.613
DG1SIFT	0.661
the proposed method	0.707

Second-Tier (ST)

Method	ST
LSD-sum	0.327
ZFDR	0.621
3DSP_L2_1000_hik	0.502
DVD+DB+GMR	0.739
DG1SIFT	0.799
the proposed method	0.827

F-Measure (F)

　I think that there is a mistake of understanding the F-Measure as the E-Measure in the page.
　

Method	F
LSD-sum	0.224
ZFDR	0.442
3DSP_L2_1000_hik	0.351
DVD+DB+GMR	0.527
DG1SIFT	0.576
the proposed method	0.599

Discounted Cumulative Gain (DCG)

　Accurately the ratio of DCG to Ideal Discounted Cumulative Gain (IDCG) is calculated.

Method	DCG/IDCG
LSD-sum	0.565
ZFDR	0.776
3DSP_L2_1000_hik	0.685
DVD+DB+GMR	0.833
DG1SIFT	0.871
the proposed method	0.905

Precision-Recall Curve (PR)

　Though the evaluation code does not support the PR, the other studies show it. In my work it is calculated by the following procedure.

1. Since one curve can be computed from one query, 1,200 curves are obtained.
2. After interpolating each curve within the range of [0, 1] with a step of 0.01, the average of a series of curves is calculated.

Average Precision (AP)

　This quantity which the other studies present is also not offered by the evaluation code. In my work, by defining the AP as the area under the precision-recall curve, it is calculated.

Method	AP
LSD-sum	0.381
ZFDR	0.650
3DSP_L2_1000_hik	0.526
DVD+DB+GMR	0.765
DG1SIFT	0.811
the proposed method	0.818

I don't know whether or not two quantities, PR and AP, are computed in exactly the same way as the other studies.